Exercício Resolvido de Movimento Unidimensional
publicidade
Uma raposa, perseguida por um galgo, tem 63 pulos de dianteira sobre o cão. O galgo dá 3 pulos enquanto a raposa dá 4 pulos, porém 6 pulos do galgo valem 10 pulos da raposa. Quantos pulos o galgo deve dar para alcançar a raposa?
Dados do problema:
- Vantagem da raposa sobre o galgo: 63 pulos de raposa;
- Proporção entre os pulos do galgo e da raposa: \( \dfrac{6\;\text{pulos de galgo}}{10\;\text{pulos de reposa}} \);
- Pulos do galgo em uma unidade de tempo: 3 pulos de galgo/unidade de tempo;
- Pulos de raposa em uma unidade de tempo: 4 pulos de raposa/unidade de tempo.
Como 6 pulos do galgo (pg) valem 10 pulos da raposa (pr), isto representa um fator de conversão (Figura 1)
\[
\begin{gather}
6\;\text{pg}=10\;\text{pr}
\end{gather}
\]

Observação: Isto é um fator de conversão como no caso em que dizemos que 1 pé = 0,3046 metros
\[
\begin{gather}
1\;\text{ft}=0,3048\;\text{m}
\end{gather}
\]
só que neste caso as unidades de medidas são pulos de galgo e de raposa.
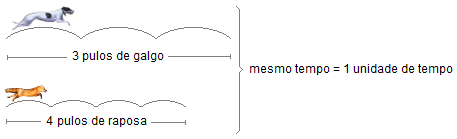
No mesmo intervalo de tempo que o galgo dá 3 pulos a raposa dá 4 pulos (Figura 2). Vamos tomar este intervalo de tempo, que é o mesmo para os dois, como sendo a unidade de tempo (ut). A velocidade do galgo será
\[
\begin{gather}
v_{g}=3\;\text{pg/ut}
\end{gather}
\]
a velocidade da raposa será
\[
\begin{gather}
v_{r}=4\;\text{pr/ut}
\end{gather}
\]
Observação: Estes dois valores representam velocidades em unidades diferentes, como se
tivéssemos dois corpos com velocidades, por exemplo
\[
\begin{gather}
v_{1}=5\;\text{ft/s}
\end{gather}
\]
\[
\begin{gather}
v_{2}=8\;\text{m/s}
\end{gather}
\]
A raposa tem 63 pulos (de raposa) de vantagem, esta é a posição inicial da raposa
\[
\begin{gather}
S_{0r}=63\;\text{pr}
\end{gather}
\]
Como queremos o número de pulos do galgo vamos converter a velocidade da raposa e a posição inicial da
raposa para pulo de galgo
\[
\begin{gather}
S_{0r}=63\;\cancel{\text{pr}}.\frac{6\;\text{pg}}{10\;\cancel{\text{pr}}}=\frac{378}{10}\;\text{pg}\\[10pt]
v_{r}=4\;\frac{\cancel{\text{pr}}}{\text{ut}}.\frac{6\;\text{pg}}{10\;\cancel{\text{pr}}}=\frac{24}{10}\;\text{pg/ut}
\end{gather}
\]
Assim podemos esquematizar o problema (Figura 3)
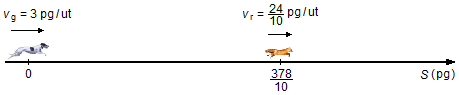
Como os dois animais têm velocidades constantes eles estão em Movimento Retilíneo Uniforme (M.R.U.), dado pela expressão
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_{0}+vt}
\end{gather}
\]
Adotamos que o galgo parte da origem, S0g=0, aplicando a expressão acima para os
dois animais
\[
\begin{gather}
S_{g}=S_{0g}+v_{g}t\\[5pt]
S_{g}=3t
\end{gather}
\]
\[
\begin{gather}
S_{r}=S_{0r}+v_{r}t\\[5pt]
S_{r}=\frac{378}{10}+\frac{24}{10}t
\end{gather}
\]
Igualando as duas expressões temos o instante em que o galgo alcança a raposa
\[
\begin{gather}
S_{g}=S_{r}\\[5pt]
3t=\frac{378}{10}+\frac{24}{10}t\\[5pt]
3t-\frac{24}{10}t=\frac{378}{10}
\end{gather}
\]
multiplicando ambos os lados da expressão por 10
\[
\begin{gather}
\qquad\qquad\quad 3t-\frac{24}{10}t=\frac{378}{10} \qquad \times{(10)}\\[5pt]
10.3t-\cancel{10}.\frac{24}{\cancel{10}}t=\cancel{10}.\frac{378}{\cancel{10}}\\[5pt]
30t-24t=378\\[5pt]
6t=378\\[5pt]
t=\frac{378}{6}\\[5pt]
t=63\;\text{ut}
\end{gather}
\]
substituindo este valor na expressão do galgo
\[
\begin{gather}
S_{g}=3.63
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{g}=189\;\text{pg}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .