Exercício Resolvido de Movimento Unidimensional
publicidade
Dois trens de 120 e 280 metros de comprimento movem-se em linhas paralelas retilíneas e com velocidades constantes. Quando os dois trens se movem no mesmo sentido são necessários 20 segundos para que o primeiro trem ultrapasse o segundo, quando se movem em sentidos opostos são necessários 10 segundos para que um passe pelo outro. Determinar as velocidades dos trens.
Dados do problema:
- Comprimento do trem 1: d1 = 120 m;
- Comprimento do trem 2: d2 = 280 m;
- Intervalo de tempo para ultrapassagem no mesmo sentido: tA = 20 s;
- Intervalo de tempo para ultrapassagem em sentidos opostos: tB = 10 s.
Os dois trens possuem dimensões relevantes para o problema eles são considerados objetos extensos.
Se eles se movem no mesmo sentido a ultrapassagem começa quando, a parte dianteira do trem de trás alcança a parte traseira do trem da frente, e termina quando, a parte traseira do primeiro trem passa pela parte da frente do segundo trem.
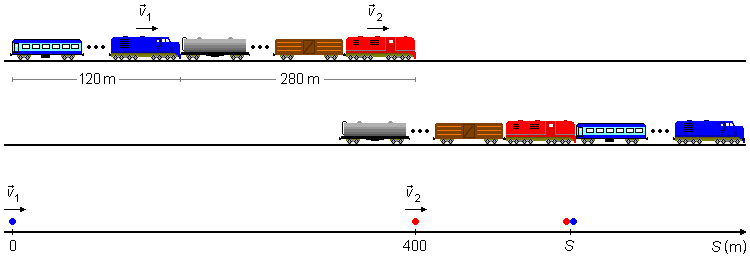
Adotamos um sistema de referência orientado para a direita. O problema pode ser reduzido a um ponto material, que representa a parte traseira do primeiro trem na origem do referencial S01 = 0 com velocidade v1, e outro ponto material que representa a parte dianteira do segundo trem, em um ponto dado pela soma dos comprimentos dos dois trens 120+280=400 m, à frente S02 = 400 m com velocidade v2. A ultrapassagem ocorre quando estes dois pontos se encontram (Figura 1).
Se eles se movem em sentidos opostos a ultrapassagem começa quando, a parte dianteira do trem de trás encontra a parte dianteira do trem da frente, e termina quando, a parte traseira do primeiro trem passa pela parte traseira do segundo trem.
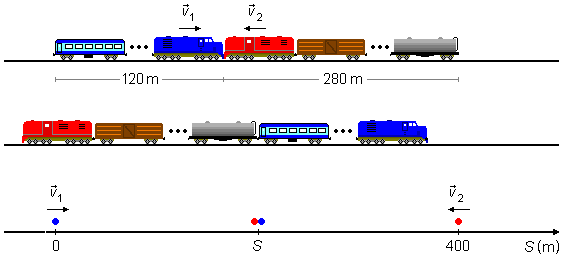
Adotamos um sistema de referência orientado para a direita. O problema pode ser reduzido a um ponto material, que representa a parte traseira do primeiro trem na origem do referencial S01 = 0 com velocidade v1, e outro ponto material que representa a parte traseira do segundo trem num ponto dado pela soma dos comprimentos dos dois trens 120+280=400 m, à frente S02 = 400 m com velocidade −v2. A ultrapassagem ocorre quando estes dois pontos se cruzam (Figura 2).
Solução
Os dois pontos estão em Movimento Retilíneo Uniforme (M.R.U.) dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_{0}+vt} \tag{I}
\end{gather}
\]
escrevendo a expressão (I) para os dois pontos se movendo no mesmo sentido (Figura 1), para o primeiro trem
\[
\begin{gather}
S_{1}=S_{01}+v_{1}t_{A}\\
S_{1}=0+v_{1}.20\\
S_{1}=20v_{1} \tag{II}
\end{gather}
\]
para o segundo trem
\[
\begin{gather}
S_{2}=S_{02}+v_{2}t_{A}\\
S_{2}=400+20v_{2} \tag{III}
\end{gather}
\]
Impondo a condição de que quando os dois móveis se encontram eles ocupam a mesma posição na trajetória
igualamos as expressões (II) e (III)
\[
\begin{gather}
S_{1}=S_{2}\\
20v_{1}=400+20v_{2}\\
20v_{1}-20v_{2}=400 \tag{IV}
\end{gather}
\]
Escrevendo a expressão dos dois pontos para o movimento em sentidos opostos (Figura 2), para o primeiro trem
\[
\begin{gather}
S_{1}=S_{01}+v_{1}t_{B}\\
S_{1}=0+v_{1}.10\\
S_{1}=10v_{1} \tag{V}
\end{gather}
\]
para o segundo trem
\[
\begin{gather}
S_{2}=S_{02}-v_{2}t_{B}\\
S_{2}=400-10v_{2} \tag{VI}
\end{gather}
\]
Impondo a condição de que quando os dois móveis se cruzam eles ocupam a mesma posição na trajetória igualamos
as expressões (IV) e (V)
\[
\begin{gather}
S_{1}=S_{2}\\
10v_{1}=400-10v_{2}\\
10v_{1}+10v_{2}=400 \tag{VII}
\end{gather}
\]
As expressões (IV) e (VII) formam um sistema de duas equações a duas incógnitas,
v1 e v2
\[
\left\{
\begin{array}{l}
20v_{1}-20v_{2}=400\\
10v_{1}+10v_{2}=400
\end{array}
\right. \tag{VIII}
\]
multiplicando a segunda equação do sistema (VIII) por 2 e somando com a primeria equação
\[
\begin{gather}
\qquad\qquad
\left\{
\begin{array}{l}
20v_{1}-20v_{2}=400\\
10v_{1}+10v_{2}=400 \qquad (\times 2)
\end{array}
\right.\\[10pt]
\frac{
\begin{align}
20v_{1}-20v_{2}&=400\quad\;\\
(+)\;20v_{1}+20v_{2}&=800\quad\;
\end{align}
}
{40v_{1}+0v_{2}=1200}\\
40v_{1}=1200\\
v_{1}=\frac{1200}{40}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{v_{1}=30\;\text{m/s}}
\]
Substituindo este valor de v1 em qualquer uma das equações do sistema (VIII), obtemos o
valor de v2, substituindo na segunda equação
\[
\begin{gather}
10.30+10v_{2}=400\\
300+10v_{2}=400\\
10v_{2}=400-300\\
10v_{2}=100\\
v_{2}=\frac{1000}{10}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{v_{2}=10\;\text{m/s}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .