Um trem de 100 m de comprimento corre paralelamente a um automóvel de dimensões desprezíveis. Seus movimentos são retilíneos, em um mesmo sentido, e a velocidade do automóvel é o dobro da velocidade do trem, ambas constantes. Qual o espaço percorrido pelo automóvel para ultrapassar o trem?


Dados do problema:

• Comprimento do trem:    d = 100 m;
• Velocidade do trem:    v_t = v;
• Velocidade do automóvel:    v_a = 2v.

Esquema do problema:

Como o automóvel possui dimensões desprezíveis, comparadas com as dimensões do trem, ele pode ser considerado um ponto material, enquanto as dimensões do trem são relevantes para o problema, ele é um objeto extenso.
A ultrapassagem começa quanto o automóvel alcança a parte traseira do trem e termina quando ele alcança a parte dianteira do trem (Figura 1).

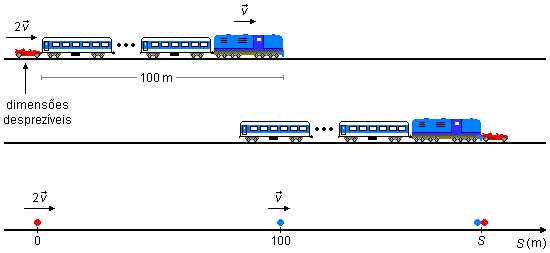
Adotando um sistema de referência orientado para a direita. O problema pode ser reduzido a um ponto material, que representa o automóvel, na origem do referencial, S_0a = 0, com velocidade 2v, e outro ponto material que representa a parte dianteira do trem 100 m a frente, S_0t = 100 m, com velocidade v. A ultrapassagem ocorre quando estes dois pontos se encontram.

Solução

Os dois pontos estão em Movimento Retilíneo Uniforme (M.R.U.) dado por escrevendo as equações horárias dos dois pontos, para o automóvel para o trem Impondo a condição de que, quando os dois móveis se encontram eles ocupam a mesma posição na trajetória, igualamos as expressões (I) e (II) este será o intervalo de tempo que a ultrapassagem leva para acontecer, substituindo este resultado em qualquer uma das equações horárias temos o espaço percorrido pelo automóvel para ultrapassar o trem, substituindo em (I)