Exercício Resolvido de Dinâmica

Home

Física

Básico Médio Superior 1 Superior 2

Novos

Básico Médio Superior 1 Superior 2

Matemática

Médio Superior

Bibliografia

FISICAEXE

Busca

Exercício Resolvido de Dinâmica

Um carrinho de massa M está unido por uma corda a uma carga de massa m. No momento inicial o carrinho tem velocidade v₀ e se move para a esquerda em um plano horizontal. Determinar:
a) O intervalo de tempo decorrido até o carrinho parar;
b) O espaço percorrido até o carrinho parar.
Considere a corda inextensível e de massa desprezível, não existe atrito no plano horizontal e na polia e adote a aceleração da gravidade igual a g.

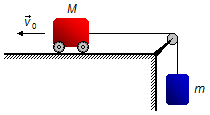
Dados do problema:

Massa do carrinho: M;
Velocidade inicial do carrinho: v₀;
Massa da carga: m;
Aceleração da gravidade: g.

Esquema do problema:

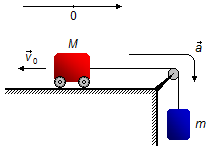
Adotamos um sistema de referência orientado para a direita e com origem no ponto onde está o carrinho inicialmente. Escolhemos a aceleração no sentido em que a carga está descendo.

Figura 1

Solução

Isolando os corpos e pesquisando as forças que agem em cada um deles aplicamos a 2.ª Lei de Newton

\begin{matrix} (I) & \vec{F} = m \vec{a} \end{matrix}

Carrinho:

Direção vertical:

${\vec{P}}_{M}$ : força peso do carrinho;
${\vec{N}}_{M}$ : força normal de reação da superfície devido ao contato das rodas.

Direção horizontal:

$\vec{T}$ : força de tensão na corda.

Na direção vertical não há movimento, a força peso

{\vec{P}}_{M}

e a força normal de reação

{\vec{N}}_{M}

se anulam.

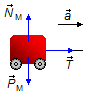
Figura 2

Na direção horizontal aplicando a expressão (I)

\begin{matrix} (II) & T = M a \end{matrix}

Carga:

${\vec{P}}_{m}$ : força peso da carga;
$\vec{T}$ : força de tensão na corda.

Na direção horizontal não há forças atuando. Na direção vertical aplicando a expressão (I)

\begin{matrix} (III) & P_{m} - T = m a \end{matrix}

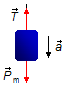
Figura 3

a) As equações (II) e (III) formam um sistema de duas equações a duas incógnitas, T e a

\begin{matrix} {\begin{cases} T = M a \\ P_{m} - T = m a \end{cases} \end{matrix}

somando as duas equações

\begin{matrix} \frac{\begin{array}{r} T = M a \\ P_{m} - T = m a \end{array}}{P_{m} = (M + m) a} \\ a = \frac{P_{m}}{M + m} \end{matrix}

A força peso é dada por

P = m g

para o peso da carga

P_{m} = m g

substituindo este valor na expressão acima para a aceleração

\begin{matrix} (IV) & a = \frac{m g}{M + m} \end{matrix}

Da situação inicial entende-se que o carrinho foi lançado por alguma força para a esquerda. Em um dado momento esta força parou de atuar, e quando se iniciou a contagem do tempo a velocidade tinha módulo v₀. No instante em que a força de lançamento para de atuar apenas a força de tração na corda, devido a carga, atua no carrinho conferindo a este uma aceleração contrária ao movimento (desaceleração), assim, o carrinho está em movimento retardado retrógrado.
O carrinho move-se inicialmente contra a orientação da trajetória, portanto, sua velocidade é negativa −v₀, no instante em que ele parar sua velocidade final será nula (v=0).
A função horária da velocidade para o Movimento Retilíneo Uniformemente Variado (M.R.U.V.) é dada por

\begin{matrix} (V) & v = v_{0} + a t \end{matrix}

substituindo a expressão (IV) e os valores das velocidades inical e final na expressão (V)

\begin{matrix} 0 = - v_{0} + \frac{m g}{M + m} t \\ \frac{m g}{M + m} t = v_{0} \end{matrix}

t = v_{0} \frac{(M + m)}{m g}

b) Usando a função horária da posição do Movimento Retilíneo Uniformemente Variado (M.R.U.V.)

\begin{matrix} (VI) & S = S_{0} + v_{0} t + \frac{a}{2} t^{2} \end{matrix}

substituindo a posição inicial, a aceleração encontrada em (IV) e o resultado do item anterior para o intervalo de tempo em (VI)

\begin{matrix} S = 0 - v_{0} [v_{0} \frac{(M + m)}{m g}] + \frac{1}{2} \frac{m g}{(M + m)} {[v_{0} \frac{(M + m)}{m g}]}^{2} \\ S = - v_{0}^{2} \frac{(M + m)}{m g} + \frac{1}{2} \frac{m g}{(M + m)} v_{0}^{2} \frac{(M + m)^{2}}{m^{2} g^{2}} \\ S = - v_{0}^{2} \frac{(M + m)}{m g} + \frac{1}{2} v_{0}^{2} \frac{(M + m)}{m g} \end{matrix}

colocando o termo

v_{0}^{2} \frac{(M + m)}{m g}

em evidência do lado direito da igualdade

S = v_{0}^{2} \frac{(M + m)}{m g} (- 1 + \frac{1}{2})

multiplicando e dividindo por 2 o fator −1 entre parênteses

\begin{matrix} S = v_{0}^{2} \frac{(M + m)}{m g} (\frac{2}{2} . (- 1) + \frac{1}{2}) \\ S = v_{0}^{2} \frac{(M + m)}{m g} (\frac{- 2 + 1}{2}) \end{matrix}

S = - \frac{1}{2} v_{0}^{2} \frac{(M + m)}{m g}

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .