Exercício Resolvido de Dinâmica
publicidade
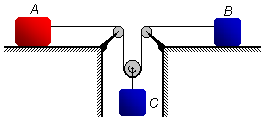
Na figura, o coeficiente de atrito entre os blocos A, B e os planos sobre os quais
deslizam é 0,2. As massas de A, B e C valem são iguais à 100 kg, 50 kg e 50 kg.
Determinar a aceleração de cada um dos blocos e a força de tensão a corda. Adote
g = 10 m/s2 e admita que
2aC = aA+aB, onde
aA, aB e aC são as acelerações dos blocos
A, B e C. A corda e as polias são ideais.
Dados do problema:
- Coeficiente de atrito entre os blocos e os planos: μ = 0,2;
- Massa do bloco A: mA = 100 kg;
- Massa do bloco B: mB = 50 kg;
- Massa do bloco C: mC = 50 kg;
- Aceleração da gravidade: g = 10 m/s2.
Adotamos um sistema de referência positivo no mesmo sentido da aceleração, para a direita para o bloco A, para a esquerda para o bloco B e para baixo para o bloco C (Figura 1-A).
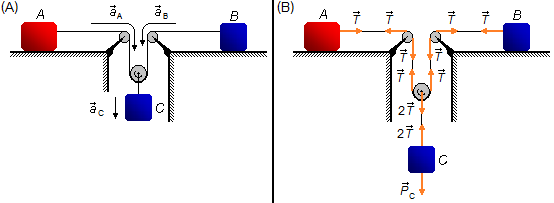
O bloco A é puxado pela tração \( \vec{T} \) que atua na corda, esta tração é transferida pela polia fixa da esquerda, para o lado esquerdo da polia móvel. Do lado direito da polia móvel temos a mesma tração \( \vec{T} \) que é transferida pela polia fixa da direita para o bloco B. Na corda que sai da polia móvel atua uma tração \( 2\vec{T} \) e esta tração é equilibrada pela força peso \( {\vec P}_{C} \) do bloco C (Figura 1-B).
Solução
Isolando os corpos e pesquisando as forças que atuam em cada um deles aplicamos a 2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{I}
\end{gather}
\]
Corpo A:
- \( {\vec P}_{A} \): força peso do bloco A;
- \( {\vec N}_{A} \) : força normal de reação do plano no bloco A;
- \( {\vec F}_{A at} \): força de atrito entre o plano e bloco A;
- \( \vec{T} \): força de tensão na corda.
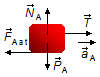
Figura 2
Na direção vertical não há movimento, a força peso \( {\vec P}_{A} \) e a força normal de reação \( {\vec N}_{A} \) se equilibram
\[
\begin{gather}
N_{A}=P_{A} \tag{II}
\end{gather}
\]
na direção horizontal aplicando a expressão (I)
\[
\begin{gather}
T-F_{A at}=m_{A}a_{A} \tag{III}
\end{gather}
\]
Corpo B:
- \( {\vec P}_{B} \): peso do bloco B;
- \( {\vec N}_{B} \): reação normal do plano no bloco B;
- \( {\vec F}_{B at} \): força de atrito entre o plano e bloco B;
- \( \vec{T} \): tração na corda.
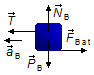
Figura 3
Na direção vertical não há movimento, a força peso \( {\vec P}_{B} \) e a força normal de reação \( {\vec N}_{B} \) se equilibram
\[
\begin{gather}
N_{B}=P_{B} \tag{IV}
\end{gather}
\]
na direção horizontal aplicando a expressão (I)
\[
\begin{gather}
T-F_{B at}=m_{B}a_{B} \tag{V}
\end{gather}
\]
Corpo C:
- \( {\vec P}_{C} \): força peso do bloco C;
- \( 2\vec{T} \): força de tensão na corda.
\[
\begin{gather}
P_{C}-2T=m_{C}a_{C} \tag{VI}
\end{gather}
\]
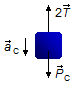
Figura 4
As equações (III), (V), (VI) e a condição dada no problema, \( 2a_{C}=a_{A}+a_{B} \), formam um sistema de quatro equações a quatro incógnitas (aA, aB, aC e T)
\[
\left\{
\begin{array}{l}
T-F_{A at}=m_{A}a_{A}\\
T-F_{B at}=m_{B}a_{B}\\
P_{C}-2T=m_{C}a_{C}\\
2a_{C}=a_{A}+a_{B}
\end{array}
\right.
\]
isolando as acelerações aA, aB, e aC nas três primeiras equações
do sistema
\[
\begin{gather}
a_{A}=\frac{T-F_{A at}}{m_{A}} \tag{VII}
\end{gather}
\]
\[
\begin{gather}
a_{B}=\frac{T-F_{B at}}{m_{B}} \tag{VIII}
\end{gather}
\]
\[
\begin{gather}
a_{C}=\frac{P_{C}-2T}{m_{C}} \tag{IX}
\end{gather}
\]
substituindo as expressões (VII), (VIII) e (IX) na quarta equação do sistema
\[
\begin{gather}
2\left(\frac{P_{C}-2T}{m_{C}}\right)=\frac{T-F_{A at}}{m_{A}}+\frac{T-F_{B at}}{m_{B}}\\
\frac{2P_{C}-4T}{m_{C}}=\frac{T-F_{A at}}{m_{A}}+\frac{T-F_{B at}}{m_{B}} \tag{X}
\end{gather}
\]
A força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{XI}
\end{gather}
\]
aplicando a expressão (XI) aos corpos A, B e C
\[
\begin{gather}
P_{A}=m_{A}g \tag{XII-a}
\end{gather}
\]
\[
\begin{gather}
P_{B}=m_{B}g \tag{XII-b}
\end{gather}
\]
\[
\begin{gather}
P_{C}=m_{C}g \tag{XII-c}
\end{gather}
\]
A força de atrito é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{at}=\mu N} \tag{XIII}
\end{gather}
\]
aplicando a expressão (XIII) aos corpos A e B
\[
F_{A at}=\mu N_{A}
\]
\[
F_{B at}=\mu N_{B}
\]
substituindo as forças normais de reação NA e NB
pelas expressões (II) e (IV)
\[
F_{A at}=\mu P_{A}
\]
\[
F_{B at}=\mu P_{B}
\]
substituindo as forças peso PA e PB
pelas expressões (XII-a) e (XII-b)
\[
\begin{gather}
F_{A at}=\mu m_{A}g \tag{XIV-a}
\end{gather}
\]
\[
\begin{gather}
F_{B at}=\mu m_{B}g \tag{XIV-b}
\end{gather}
\]
Substituindo as expressões (XII-c), (XIV-a) e (XIV-b) em (X)
\[
\frac{2m_{C}g-4T}{m_{C}}=\frac{T-\mu m_{A}g}{m_{A}}+\frac{T-\mu m_{B}g}{m_{B}}
\]
substituindo os valores numéricos dados no problema
\[
\begin{gather}
\frac{2.50.10-4T}{50}=\frac{T-0,2.100.10}{100}+\frac{T-0,2.50.10}{50}\\
\frac{1000-4T}{50}=\frac{T-200}{100}+\frac{T-100}{50}
\end{gather}
\]
multiplicando por 2 o numerador e o denominador do termo do lado esquerdo da igualdade e o segundo termo
do lado direito
\[
\begin{gather}
\frac{1000-4T}{50}.\frac{2}{2}=\frac{T-200}{100}+\frac{T-100}{50}.\frac{2}{2}\\
\frac{2000-8T}{\cancel{100}}=\frac{T-200}{\cancel{100}}+\frac{2T-200}{\cancel{100}}\\
2000-8T=T-200+2T-200\\
2000+200+200=T+2T+8T\\
11T=2400\\
T=\frac{2400}{11}\\
T=218,2\;\text{N}
\end{gather}
\]
A tração na corda presa aos corpos A e B será de
T = 218,2 N,
a tração na corda presa ao corpo C e na polia móvel será de
2T = 2.218,2 = 436,4 N.
Substituindo as forças peso dadas pelas expressões em (XII) e as forças de atrito dadas em (XIV) nas expressões (VII), (VIII) e (IX), a tração obtida acima e os dados do problema obtemos as acelerações dos blocos
\[
\begin{gather}
a_{A}=\frac{T-\mu N_{A}}{m_{A}}\\
a_{A}=\frac{T-\mu
m_{A}g}{m_{A}}\\
a_{A}=\frac{218,2-0,2.100.10}{100}\\
a_{A}=\frac{218,2-200}{100}\\
a_{A}=\frac{18,2}{100}\\
a_{A}=0,182
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{A} \simeq 0,2\;\text{m/s}^{2}}
\]
\[
\begin{gather}
a_{B}=\frac{T-\mu N_{B}}{m_{B}}\\
a_{B}=\frac{T-\mu
m_{B}g}{m_{B}}\\
a_{B}=\frac{218,2-0,2.50.10}{50}\\
a_{B}=\frac{218,2-100}{50}\\
a_{B}=\frac{118,2}{50}\\
a_{B}=2,364
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{B}\simeq 2,4\;\text{m/s}^{2}}
\]
\[
\begin{gather}
a_{C}=\frac{m_{C}g-2T}{m_{C}}\\
a_{C}=\frac{50.10-2.218,2}{50}\\
a_{C}=\frac{500-436,4}{50}\\
a_{C}=\frac{63,6}{50}\\
a_{C}=1,272
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{C}=1,3\;\text{m/s}^{2}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .