Exercício Resolvido de Dinâmica
publicidade
No sistema da figura as massas de A, B e C valem, respectivamente, 10 kg, 20 kg e
5 kg e o sen θ = 0,8. Desprezando os atritos, calcular a aceleração do conjunto e a intensidade
das forças de tração nas cordas. Adotar g = 10 m/s2.
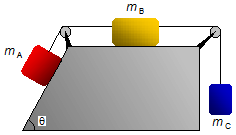
Dados do problema:
- Massa do corpo A: mA = 10 kg;
- Massa do corpo B: mB = 20 kg;
- Massa do corpo C: mC = 5 kg;
- Aceleração da gravidade: g = 10 m/s2.
Escolhemos a aceleração do sistema no sentido em que o corpo A está descendo e o corpo C
está subindo (Figura 1).
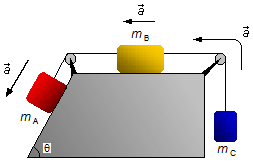
Solução
Isolamos os corpos e pesquisamos as forças que atuam em cada um deles.
Corpo A (Figura 2-A):
- \( {\vec P}_{A} \): força peso do corpo A;
- \( {\vec N}_{A} \): força normal de reação do plano no corpo A;
- \( {\vec T}_{AB} \): força de tensão na corda entre os blocos A e B.
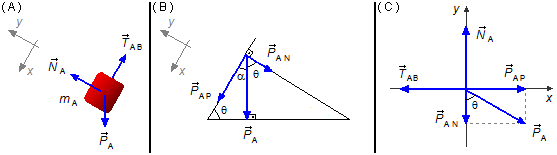
No triângulo à esquerda na Figura 2-B vemos que a força peso é perpendicular ao plano horizontal, forma um ângulo de 90º, o ângulo entre o plano inclinado e o plano horizontal é dado igual à θ. Como os ângulos internos de um triângulo devem somar 180°, o ângulo entre a força peso \( {\vec P}_{A} \) e a componente paralela \( {\vec P}_{AP} \) será
\[ \alpha +\theta +90°=180°\Rightarrow \alpha=180°-\theta -90°\Rightarrow \alpha=90°-\theta \]
As componentes do peso nas direções x e y são perpendiculares entre si, no triângulo à
direita o ângulo entre a força peso
\( \vec{P}_{A} \)
e a componente normal da força peso
\( {\vec P}_{AN} \)
será
\[ 90°-\alpha \Rightarrow 90°-(90°-\theta)\Rightarrow 90°-90°+\theta \Rightarrow \theta \]
Desenhando as forças num sistema de eixos coordenados xy (Figura 2-C), aplicamos a
2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{I}
\end{gather}
\]
Na direção y não há movimento, a força normal de reação
\( {\vec N}_{A} \)
e a componente normal da força peso
\( {\vec P}_{AN} \)
se anulam.Na direção x, considerando o ângulo θ medido a partir do eixo-y ao contrário do que se faz usualmente quando se mede o ângulo com o eixo-x
\[
\begin{gather}
P_{AP}-T_{AB}=m_{A}a \tag{II}
\end{gather}
\]
a componente paralela ao eixo-x é dada por
\[
\begin{gather}
P_{AP}=P_{A}\operatorname{sen}\theta \tag{III}
\end{gather}
\]
substituindo a expressão (III) na expressão (II)
\[
\begin{gather}
P_{A}\operatorname{sen}\theta -T_{AB}=m_{A}a \tag{IV}
\end{gather}
\]
A força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (IV) para o corpo A
\[
\begin{gather}
m_{A}g\operatorname{sen}\theta -T_{AB}=m_{A}a \tag{VI}
\end{gather}
\]
Corpo B:
- \( {\vec P}_{B} \): força peso do corpo B;
- \( {\vec N}_{B} \): força normal de reação da superfície.
- \( {\vec T}_{AB} \): força de tensão na corda entre os blocos A e B;
- \( {\vec T}_{BC} \): força de tensão na corda entre os blocos B e C.
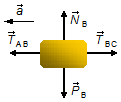
Figura 3
Na direção x, aplicando a expressão (I)
\[
\begin{gather}
T_{AB}-T_{BC}=m_{B}a \tag{VII}
\end{gather}
\]
Corpo C:
- \( {\vec{P}}_{C} \): força peso do corpo C;
- \( {\vec{T}}_{BC} \): força de tensão na corda entre os blocos B e C.
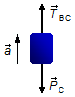
Figura 4
Na direção vertical, aplicando a expressão (I)
\[
\begin{gather}
T_{BC}-P_{C}=m_{C}a \tag{VIII}
\end{gather}
\]
substituindo a expressão (V) na expressão (VIII) para o corpo C
\[
\begin{gather}
T_{BC}-m_{C}g=m_{C}a \tag{IX}
\end{gather}
\]
As equações (VI), (VII) e (IX) formam um sistema de três equações a três incógnitas (TAB,
TBC e a)
\[
\left\{
\begin{array}{l}
m_{A}g\operatorname{sen}\theta-T_{AB}=m_{A}a\\
T_{AB}-T_{BC}=m_{B}a\\
T_{BC}-m_{C}g=m_{C}a
\end{array} \tag{X}
\right.
\]
somando as três equações
\[
\begin{gather}
\frac{
\begin{align}
m_{A}g\operatorname{sen}\theta-\cancel{T_{AB}}=m_{A}a\\
\cancel{T_{AB}}-\cancel{T_{BC}}=m_{B}a\\
\text{(+)}\qquad\cancel{T_{BC}}-m_{C}g=m_{C}a
\end{align}
}
{m_{A}g\operatorname{sen}\theta-m_{C}g=\left(m_{A}+m_{B}+m_{C}\right)a}\\
a=\frac{m_{A}g\operatorname{sen}\theta-m_{C}g}{m_{A}+m_{B}+m_{C}} \tag{XI}
\end{gather}
\]
substituindo os valores dados no problema na expressão (XI)
\[
\begin{gather}
a=\frac{10.10.0,8-5.10}{10+20+5}\\
a=\frac{80-50}{35}\\
a=\frac{30}{35}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a=0,86\;\text{m/s}^{2}}
\]
Substituindo a massa do corpo A, o valor do seno θ e a aceleração encontrada acima, na
primeira equação do sistema (X), a tensão na corda será
\[
\begin{gather}
m_{A}g\operatorname{sen}\theta-T_{AB}=m_{A}a\\
10.10.0,8-T_{AB}=10.0,86\\
80-T_{AB}=8,6\\
T_{AB}=80-8,6
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{AB}=71,4\;\text{N}}
\]
Substituindo a massa do corpo C e a aceleração, encontrada acima, na terceira equação do sistema (X),
a tensão na corda será
\[
\begin{gather}
T_{BC}-m_{C}g=m_{C}a\\
T_{BC}-5.10=3.0,86\\
T_{BC}-50=2,58\\
T_{BC}=50+2,58
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{BC}=52,6\;\text{N}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .