Exercício Resolvido de Centro de Massa
publicidade
Dos extremos de uma plataforma de comprimento L, apoiada sobre roletes sem atrito, um adulto e uma criança estão correndo um em direção ao outro. Determinar de quanto deslizará a plataforma, quando o adulto passar de um extremo ao outro da plataforma. Sabe-se que a velocidade do adulto é o dobro da velocidade da criança, as massas da plataforma, do adulto e da criança são m1, m2 e m3, respectivamente.
Dados do problema:
- Comprimento da plataforma: L;
- Massa da plataforma: m1;
- Massa do adulto: m2;
- Velocidade do adulto: v2;
- Massa da criança: m3;
- Velocidade da criança: v3.
A posição do centro de massa de um sistema de três partículas é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{x_{cm}=\frac{m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}}{m_{1}+m_{2}+m_{3}}} \tag{I}
\end{gather}
\]
Na primeira situação (Figura 1), temos um sistema de referência orientado para a direita com
origem no ponto da plataforma onde o homem está inicialmente. “Esquecendo” a plataforma, o homem e a criança,
e considerando apenas os seus centros de massa, cp para o centro de massa da plataforma, ch
para o centro de massa do homem e cc para o centro de massa da criança, o centro de massa do homem
está na posição de origem do sistema x2 = 0, o centro de massa da plataforma, de
comprimento L, está na metade do seu comprimento
\( x_{1}=\frac{L}{2} \)
e o centro de massa da criança está na ponta da plataforma oposta ao homem x3 = L.
Assim substituindo esses valores na expressão (I), temos para o centro de massa do conjunto
plataforma-homem-criança na situação inicial
\[
\begin{gather}
x_{i}=\frac{m_{1}\dfrac{L}{2}+m_{2}.0+m_{3}L}{m_{1}+m_{2}+m_{3}}\\[5pt]
x_{i}=\frac{m_{1}\dfrac{L}{2}+m_{3}L}{m_{1}+m_{2}+m_{3}}
\end{gather}
\]
multiplicando e dividindo o segundo termo do numerador do lado direito da igualdade por 2
\[
\begin{gather}
x_{i}=\frac{m_{1}\dfrac{L}{2}+\dfrac{2}{2}m_{3}L}{m_{1}+m_{2}+m_{3}}\\[5pt]
x_{i}=\frac{m_{1}\dfrac{L}{2}+2m_{3}\dfrac{L}{2}}{m_{1}+m_{2}+m_{3}}
\end{gather}
\]
colocando
\( \dfrac{L}{2} \)
em evidência no numerador
\[
\begin{gather}
x_{i}=\frac{L}{2}\left(\frac{m_{1}+2m_{3}}{m_{1}+m_{2}+m_{3}}\right) \tag{II}
\end{gather}
\]
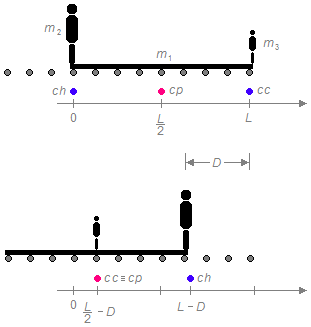
Na segunda parte da Figura 1 temos a situação final, o homem andou para frente o comprimento L da plataforma, como a velocidade da criança é metade da velocidade do homem ela andou até a metade do comprimento da plataforma enquanto isso a plataforma se deslocou de uma certa distância D para trás em relação ao homem. Assim o centro de massa do homem está na posição \( x_{2}=L-D \) e o centro de massa da plataforma e da criança coincidem estando em \( x_{1}=x_{3}=\dfrac{L}{2}-D \), novamente substituindo esses valores na expressão (I) para a situação final
\[
\begin{gather}
x_{f}=\frac{m_{1}\left(\dfrac{L}{2}-D\right)+m_{2}(L-D)+m_{3}\left(\dfrac{L}{2}-D\right)}{m_{1}+m_{2}+m_{3}}\\[5pt]
x_{f}=\frac{m_{1}\dfrac{L}{2}-m_{1}D+m_{2}L-m_{2}D+m_{3}\dfrac{L}{2}-m_{3}D}{m_{1}+m_{2}+m_{3}}
\end{gather}
\]
multiplicando e dividindo o terceiro termo do numerador do lado direito da igualdade por 2
\[
\begin{gather}
x_{f}=\frac{m_{1}\dfrac{L}{2}-m_{1}D+\dfrac{2}{2}m_{2}L-m_{2}D+m_{3}\dfrac{L}{2}-m_{3}D}{m_{1}+m_{2}+m_{3}}\\[5pt]
x_{f}=\frac{m_{1}\dfrac{L}{2}-m_{1}D+2m_{2}\dfrac{L}{2}-m_{2}D+m_{3}\dfrac{L}{2}-m_{3}D}{m_{1}+m_{2}+m_{3}}
\end{gather}
\]
colocando −D e
\( \dfrac{L}{2} \)
em evidência no numerador do lado direito da igualdade
\[
\begin{gather}
x_{f}=\frac{\dfrac{L}{2}(m_{1}+2m_{2}+m_{3})-D(m_{1}+m_{2}+m_{3})}{m_{1}+m_{2}+m_{3}} \tag{III}
\end{gather}
\]
O Centro de Massa continua na mesma posição, igualando as expressões (II) e (III)
\[
\begin{gather}
x_{i}=x_{f}\\[5pt]
\frac{L}{2}\left(\frac{m_{1}+2m_{3}}{\cancel{m_{1}+m_{2}+m_{3}}}\right)=\frac{\dfrac{L}{2}(m_{1}+2m_{2}+m_{3})-D(m_{1}+m_{2}+m_{3})}{\cancel{m_{1}+m_{2}+m_{3}}}\\[5pt]
\frac{L}{2}(m_{1}+2m_{3})=\frac{L}{2}(m_{1}+2m_{2}+m_{3})-D(m_{1}+m_{2}+m_{3})\\[5pt]
D(m_{1}+m_{2}+m_{3})=\frac{L}{2}(m_{1}+2m_{2}+m_{3})-\frac{L}{2}(m_{1}+2m_{3})
\end{gather}
\]
colocando
\( \dfrac{L}{2} \)
em evidência do lado direito da igualdade
\[
\begin{gather}
D(m_{1}+m_{2}+m_{3})=\frac{L}{2}(m_{1}+2m_{2}+m_{3}-m_{1}-2m_{3})\\[5pt]
D(m_{1}+m_{3}+m_{2})=\frac{L}{2}(2m_{2}-m_{3})
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{D=\frac{2m_{2}-m_{3}}{m_{1}+m_{3}+m_{2}}\frac{L}{2}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .