Exercício Resolvido de Resistores
publicidade
Entre os terminais A e B da figura aplica-se uma d.d.p. de 200 V. Calcule as
intensidades das correntes em cada resistor e o resistor equivalente.

Dados do problema:
- Diferença de potencial entre A e B: VAB = 220 V.
Solução
Os dois resistores de 10 Ω, colocados entre os pontos D e B, estão ligados em
paralelo (Figura 1). O resistor equivalente para resistores iguais é dado por
\[ \bbox[#99CCFF,10px]
{ R_{eq}=\frac{R}{n}}
\]
para n = 2
\[
\begin{gather}
R_{1}=\frac{10}{2}\\
R_{1}=5\;\Omega \tag{I}
\end{gather}
\]
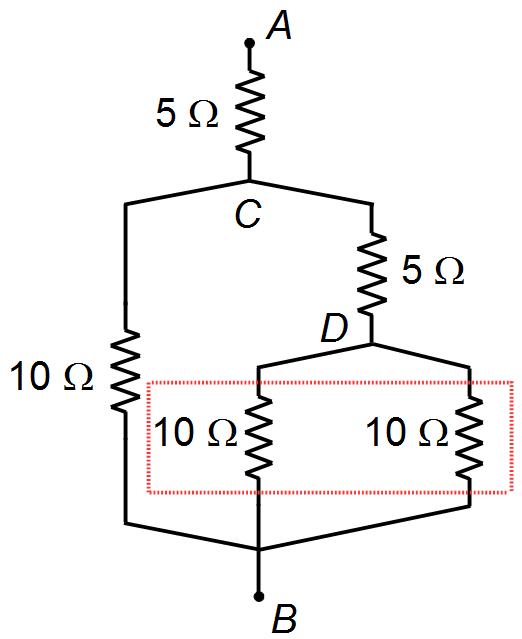
Figura 1
Observação: Também poderíamos determinar o resistor equivalente aplicando a expressão para
dois resistores quaisquer em paralelo
\[ \bbox[#99CCFF,10px]
{R_{eq}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}}
\]
\[
\begin{gather}
R_{1}=\frac{10.10}{10+10}\\
R_{1}=\frac{10}{20}\\
R_{1}=5\;\Omega
\end{gather}
\]
Ou poderíamos determinar o resistor equivalente aplicando a expressão geral para associação de resistores
em paralelo
\[ \bbox[#99CCFF,10px]
{\frac{1}{R_{eq}}=\sum_{i=1}^{n}{\frac{1}{R_{i}}}}
\]
\[
\begin{gather}
\frac{1}{R_{1}}=\frac{1}{10}+\frac{1}{10}\\
\frac{1}{R_{1}}=\frac{10+10}{10.10}\\
\frac{1}{R_{1}}=\frac{20}{100}\\
R_{1}=\frac{100}{20}\\
R_{1}=5\;\Omega
\end{gather}
\]
Os dois resistores de 5 Ω entre os pontos C e B estão ligados em série (Figura 2).
O resistor equivalente para resistores iguais é dado por
\[ \bbox[#99CCFF,10px]
{R_{eq}=nR}
\]
para n = 2
\[
\begin{gather}
R_{2}=2.5\\
R_{2}=10\;\Omega \tag{II}
\end{gather}
\]
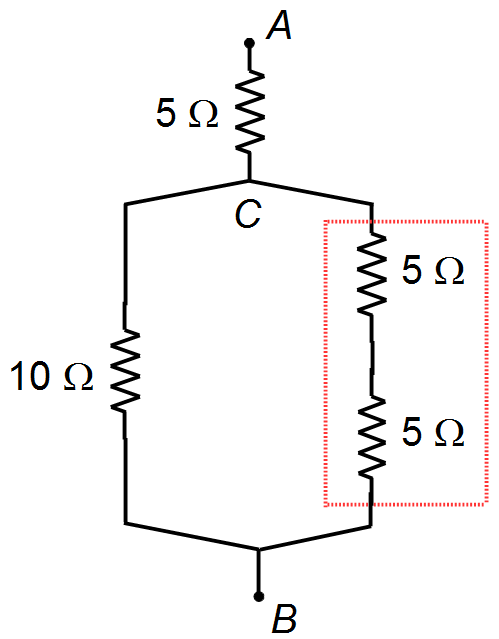
Figura 2
Observação: Também poderíamos determinar o resistor equivalente aplicando a expressão geral
para associação de resistores em série
\[ \bbox[#99CCFF,10px]
{R_{eq}=\sum_{i=1}^{n}R_{i}}
\]
\[
\begin{gather}
R_{3}=5+5\\
R_{3}=10\;\Omega
\end{gather}
\]
Para os dois resistores em paralelo entre os pontos C e B (Figura 3) vale o mesmo
resultado (I) acima
\[
R_{4}=5\;\Omega
\]
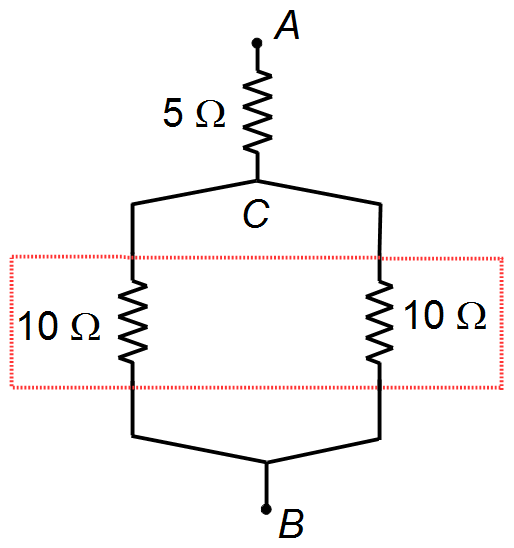
Figura 3
Para os dois resistores em série entre os pontos A e B (Figura 4) vale o mesmo resultado
(II) acima, que é o resistor equivalente do circuito
\[ \bbox[#FFCCCC,10px]
{R_{eq}=10\;\Omega}
\]
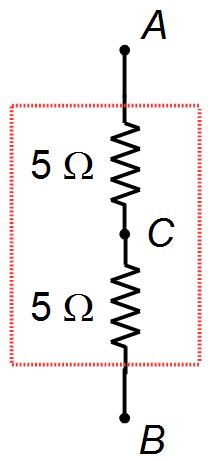
Figura 4
A 1.ª Lei de Ohm é dada por
\[ \bbox[#99CCFF,10px]
{U=ri}
\]
substituindo U = VAB = 220 V e r = Req = 10 Ω
(Figura 5)
\[
\begin{gather}
V_{AB}=R_{eq}i\\
i=\frac{V_{AB}}{R_{eq}}\\
i=\frac{200}{10}\\
i=20\;\text{A}
\end{gather}
\]
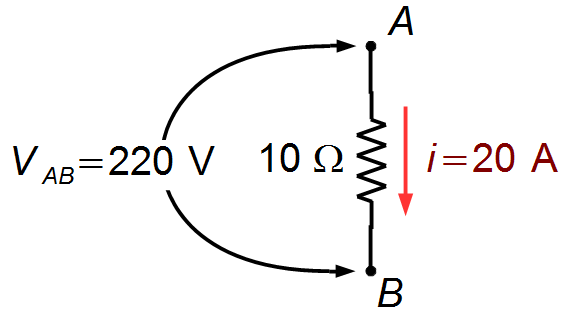
Figura 5
Voltando para o circuito da Figura 4 temos dois resistores em série, neste caso os dois resistores são
percorridos pela mesma corrente (Figura 6)
\[ \bbox[#FFCCCC,10px]
{i_{1}=20\;\text{A}}
\]
\[
i_{2}=20\;\text{A}
\]
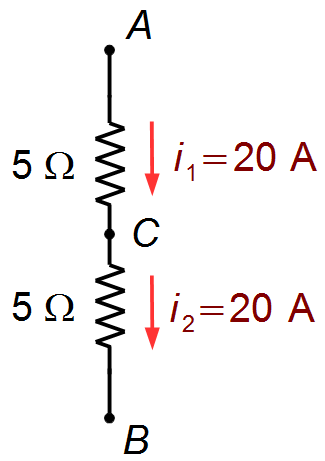
Figura 6
Voltando para o circuito da Figura 3 temos dois resistores de mesmo valor ligados em paralelo entre os
pontos C e B, neste caso a corrente i2 se divide igualmente entre os
dois resistores (Figura 7)
\[
\begin{gather}
i_{3}=i_{4}=\frac{i_{2}}{2}\\
i_{3}=i_{4}=\frac{20}{2}\\
i_{3}=i_{4}=10\;\text{A}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{i_{3}=10\;\text{A}}
\]
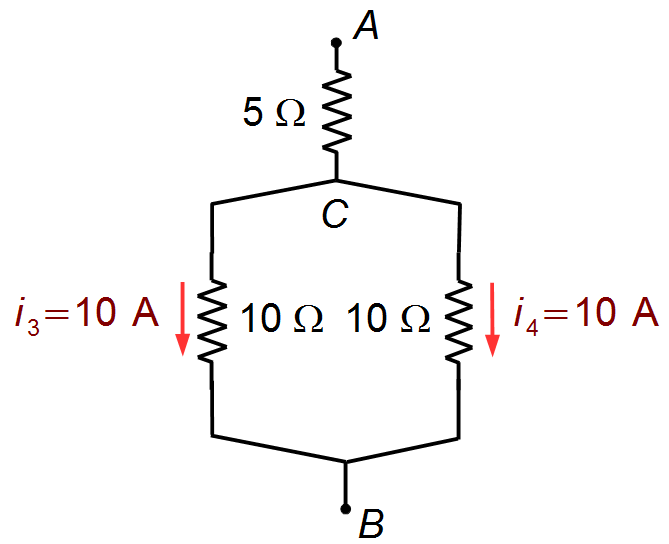
Figura 7
Voltando para o circuito da Figura 2 temos dois resistores em série, neste caso os dois resistores são
percorridos pela mesma corrente (Figura 8)
\[ \bbox[#FFCCCC,10px]
{i_{5}=10\;\text{A}}
\]
\[
i_{6}=10\;\text{A}
\]
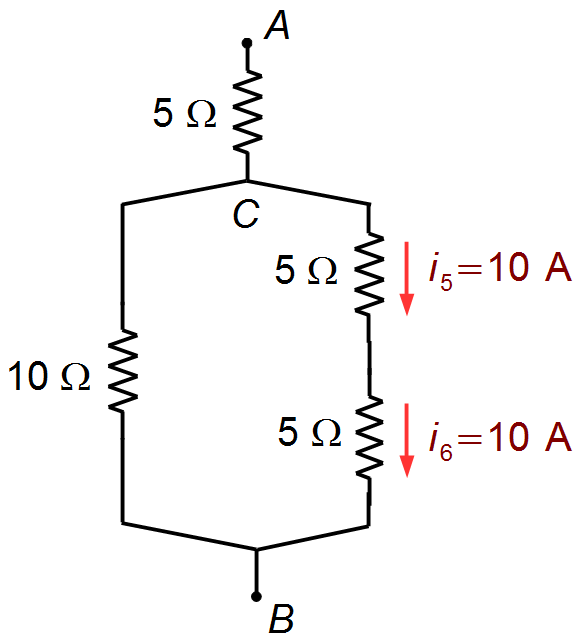
Figura 8
Voltando para o circuito da Figura 1 temos dois resistores de mesmo valor ligados em paralelo entre os
pontos D e B, neste caso a corrente i6 se divide igualmente entre os
dois resistores (Figura 9)
\[
\begin{gather}
i_{7}=i_{8}=\frac{i_{6}}{2}\\
i_{7}=i_{8}=\frac{10}{2}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{i_{7}=i_{8}=5\;\text{A}}
\]
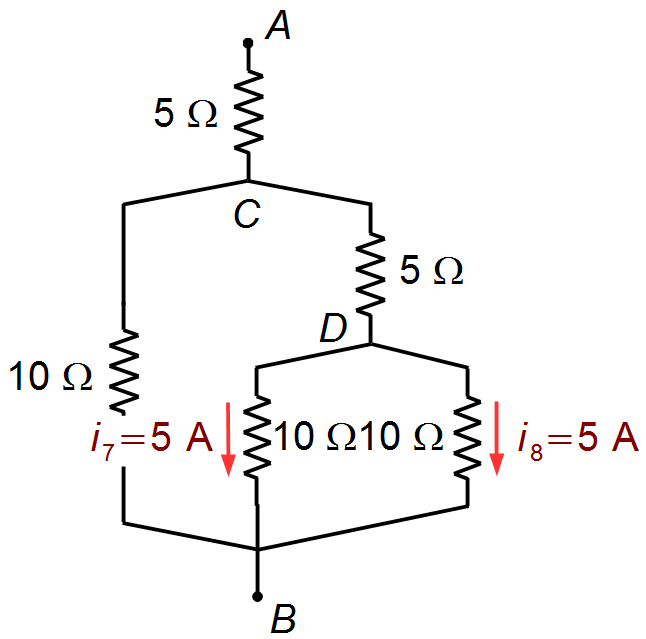
Figura 9
O esquema completo de correntes será (Figura 10)
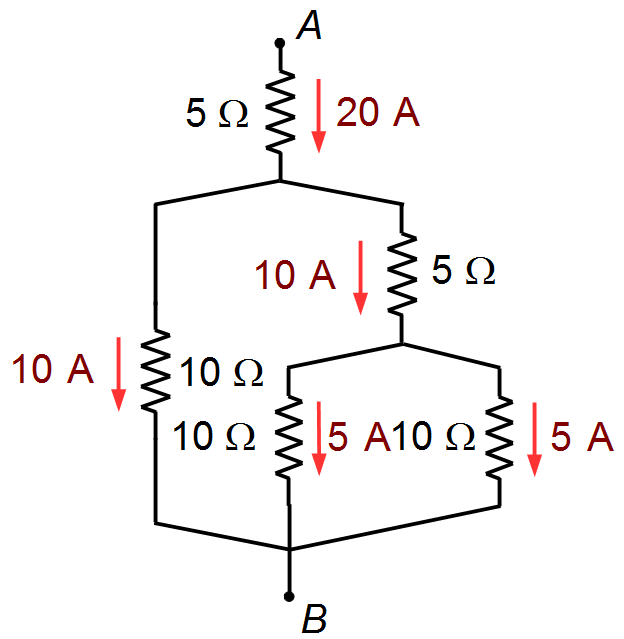
Figura 10
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .