No circuito abaixo, determinar as correntes nos ramos e seus verdadeiros sentidos.

Dados do problema:
Resistores:
- R1 = 0,5 Ω;
- R2 = 0,5 Ω;
- R3 = 1 Ω;
- R4 = 0,5 Ω;
- R5 = 0,5 Ω;
- R6 = 3 Ω;
- R7 = 1 Ω.
Baterias:
- E1 = 20 V;
- E2 = 20 V;
- E3 = 6 V;
Solução:
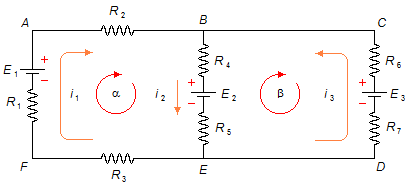
Em primeiro lugar, a cada ramo do circuito atribuímos, aleatoriamente, um sentido de corrente. No ramo EFAB temos a corrente i1 no sentido horário, no ramo BE a corrente i2 de B para E e no ramo EDCB a corrente i3 no sentido anti-horário. Em segundo lugar. para cada malha do circuito atribuímos um sentido, também aleatório, para percorrer a malha. Para a malha α (ABEFA) sentido horário e para a malha β (BCDEB) também sentido horário (Figura 1).
- Aplicando a Lei dos Nós
As correntes i1 e i3 chegam no nó B e a corrente i2 sai dele
- Aplicando a Lei das Malhas
Para a malha α a partir do ponto A no sentido escolhido, esquecendo a malha β (Figura 2)

substituindo os valores do problema
Para a malha β a partir do ponto B no sentido escolhido, esquecendo a malha α (Figura 3)

substituindo os valores
As equações (I), (II) e (III) formam um sistema de três equações a três incógnitas (i1, i2 e i3)
isolando o valor de i1 na segunda equação
isolando o valor de i3 na terceira equação
substituindo as expressões (IV) e (V) na primeira equação
multiplicando a equação por 4
substituindo o valor (VI) encontrado acima, nas expressões (IV) e (V) encontramos os valores de i1 e i3
Como o valor das correntes i2 e i3 são negativas, isto indica que seus verdadeiros sentidos são contrários àqueles escolhidos na Figura 1. Os valores das correntes são i1=1 A, i2=2 A, e i3=3 A, e seus sentidos estão mostrados na Figura 4.


Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .