Exercício Resolvido de Movimento Circular
DE
EN
ES
FR
IT
publicidade
Um garoto gira, sobre sua cabeça, uma pedra amarrada a um cordão com velocidade escalar constante, o raio
descrito pela circunferência feita pela pedra é de 1 m e faz uma volta em 2 s. Determine:
a) A velocidade escalar da pedra;
b) O módulo da aceleração centrípeta que atua na pedra.
a) A velocidade escalar da pedra;
b) O módulo da aceleração centrípeta que atua na pedra.
Dados do problema:
- Raio da trajetória: R = 1 m;
- Período de rotação: T = 2 s.
Esquema do problema:
No sistema temos a velocidade \( \vec v \) que é tangente à trajetória, e a aceleração centrípeta \( {\vec a}_{cp} \) que atua na direção da corda, com sentido voltado para o centro da circunferência. A aceleração centrípeta é responsável por alterar a direção da velocidade escalar (ela faz com que a pedra faça a curva).
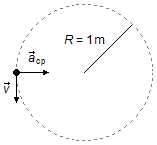
No sistema temos a velocidade \( \vec v \) que é tangente à trajetória, e a aceleração centrípeta \( {\vec a}_{cp} \) que atua na direção da corda, com sentido voltado para o centro da circunferência. A aceleração centrípeta é responsável por alterar a direção da velocidade escalar (ela faz com que a pedra faça a curva).
Solução:
a) A velocidade escalar é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r} \tag{I}
\end{gather}
\]
onde ω é a velocidade angular dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega=\frac{2\pi}{T}} \tag{II}
\end{gather}
\]
substituindo a equação (II) na equação (I)
\[
\begin{gather}
v=\frac{2\pi}{T}r
\end{gather}
\]
substituindo os dados do problema e usando π = 3,14
\[
\begin{gather}
v=\frac{\cancel 2\times 3,14}{\cancel 2}\times 1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=3,14\;\mathrm{m/s}}
\end{gather}
\]
b) O módulo da aceleração centrípeta é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{3,14^2}{1} \\[5pt]
|\;a_{cp}\;|=\frac{9,86}{1}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{|\;a_{cp}\;|\approx 9,86\;\mathrm{m/s^2}}
\end{gather}
\]
publicidade