a) F = 400 N;
b) F = 720 N;
c) F = 1200 N.
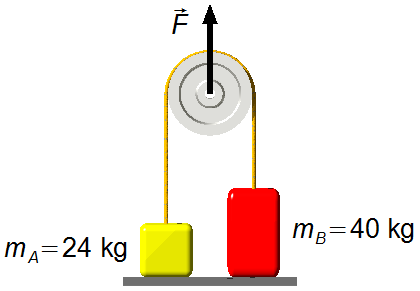
Dados do problema:
- Massa do corpo A: ma = 24 kg;
- Massa do corpo B: mb = 40 kg;
- Aceleração da gravidade: g = 9,8 m/s2.
Esquema do problema:
Adotamos um sistema de referência orientado positivamente no mesmo sentido da força
\( \vec F \).
A força aplicada em uma polia se divide igualmente entre os dois lados (Figura 1-A), assim a força de cada
lado da polia será
\( \frac{\vec F}{2} \).
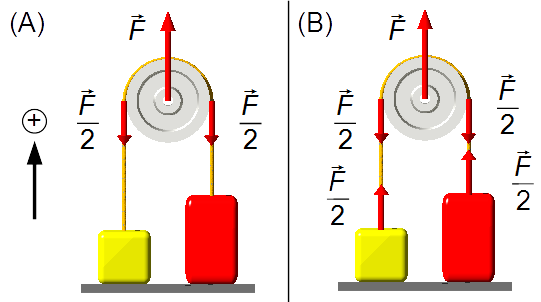
Como a corda é ideal, de massa desprezível e inextensível, ela somente transmite a força na polia para os
corpos. A componente da força
\( \vec F \)
sobre cada corpo será
\( \frac{\vec F}{2} \)
(Figura 1-B).
Fazendo um Diagrama de Corpo Livre, temos as forças que atuam nos blocos.
-
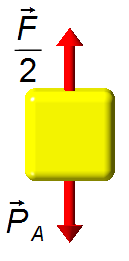
Corpo A (Figura 2):
- \( \dfrac{\vec F}{2} \): força transmitida da polia;
- \( {\vec P}_a \): peso do corpo A.
-
Corpo B (Figura 3):
- \( \dfrac{\vec F}{2} \): força transmitida da polia;
- \( {\vec P}_b \): peso do corpo B.

Solução:
Aplicando a 2.ª Lei de Newton
- Corpo A:
- Corpo B:
A força peso é dada por
para os corpos A e B
substituindo a equação (III) na equação (I)
substituindo a equação (IV) na equação (II)
a) Para \( F=400\;\text N \), a aceleração do corpo A é dada pela equação (V)
A aceleração do corpo B é dada pela equação (VI)
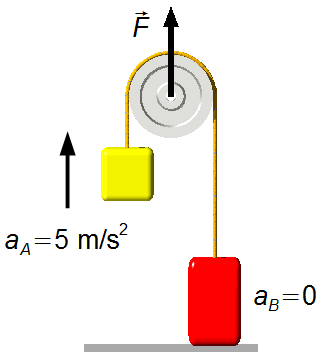
b) Para \( F=720\;\text N \), a aceleração do corpo A é dada pela equação (V)
A aceleração do corpo B é dada pela equação (VI)
c) Para \( F=1200\;\text N \), a aceleração do corpo A é dada pela equação (V)
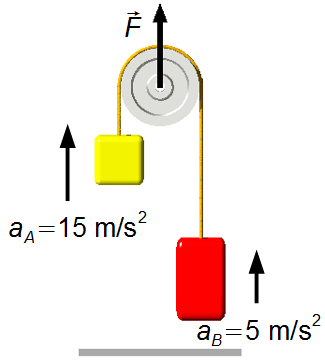
O corpo A tem aceleração
e o corpo B tem aceleração

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .