Ejercicio Resuelto sobre Dinámica

Un cuerpo, de masa igual a 2 kg con velocidad inicial de 10 m/s en sentido positivo, está bajo la acción de una fuerza variable en función de la posición, dada por

\[ \begin{gather} F_x=-8x \qquad\qquad\text{unidades (SI)} \end{gather} \]

¿Cuál será la distancia recorrida por ese cuerpo hasta que su velocidad sea igual a cero?

Datos del problema:

Masa del cuerpo: m = 2 kg;
Velocidad inicial del cuerpo: v₀ = 10.

Esquema del problema:

Tomamos un sistema de referencia con el eje Ox orientado hacia la derecha y el eje Oy hacia arriba (Figura 1).

Figura 1

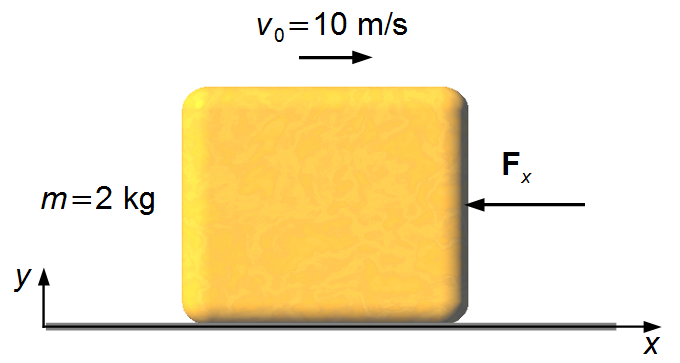
La fuerza dada es negativa, es una fuerza de resistencia que está en la dirección opuesta al movimiento. La fuerza actúa disminuyendo la velocidad del cuerpo hasta que su velocidad final sea igual a cero.

Solución:

Aplicando la Segunda Ley de Newton en la dirección x, la fuerza dada en el problema es la única fuerza en esta dirección.

\[ \begin{gather} \bbox[#99CCFF,10px] {\mathbf F=m\frac{d\mathbf v}{dt}} \end{gather} \]

\[ \begin{gather} F_x=m\frac{dv_x}{dt}\\[5pt] -8x=2\frac{dv_x}{dt} \end{gather} \]

multiplicando y dividiendo el lado derecho de la ecuación por dx

\[ \begin{gather} -4x=\frac{dv_x}{dt}\frac{dx}{dx} \end{gather} \]

invirtiendo el orden de los términos de integración en el denominador

\[ \begin{gather} -4x=\frac{dv_x}{dx}\frac{dx}{dt} \end{gather} \]

aplicando la definición de velocidad

\[ \begin{gather} \bbox[#99CCFF,10px] {v=\frac{dx}{dt}} \end{gather} \]

integrando en dx ambos lados de la igualdad

\[ \begin{gather} \int -4x\;dx=\int v_x\frac{dv_x}{dx}\;dx\\[5pt] \int-4x\;dx=\int v_x\;dv_x \end{gather} \]

El factor constante (−4) sale de la integral en el lado izquierdo. Los limites de integración son 0, posición inicial, hasta x en un instante cualquiera en dx, y 10 m/s, velocidad inicial, hasta 0, velocidad final en dvx dv_x.

\[ \begin{gather} -4\int_0^x x'\;dx'=\int_{10}^0 v_x\;dv_x \end{gather} \]

Integral de \( \displaystyle \int_0^x x'\;dx' \)

\[ \begin{gather} \int_0^x x'\;dx'=\left.\frac{x^{1+1}}{1+1}\right|_0^x =\frac{x^2}{2}-\frac{0^2}{2}=\frac{x^2}{2} \end{gather} \]

Integral de \( \displaystyle \int_{10}^0v_x\;dv_x \)

\[ \begin{gather} \int_{10}^0 v_x\;dv_x=\left.\frac{v_x^{1+1}}{1+1}\right|_{10}^0=\frac{0^2}{2}-\frac{10^2}{2}=\frac{100}{2}=50 \end{gather} \]

\[ \begin{gather} -\cancelto{2}{4}\times\frac{x^2}{\cancel 2}=-50\\[5pt] x^2=\frac{-50}{-2}\\[5pt] x=\sqrt{25\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {x=5\;\mathrm m} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .