Ejercicio Resuelto sobre Dinámica

Solución 2 del problema:

La ecuación de la velocidad en función de la posición v(x) está dada por

\[ \begin{gather} \bbox[5px,border:5px solid #99CCFF] {v^2(x)=-4x^2+100} \tag{I} \end{gather} \]

Solución 3 del problema:

Las ecuaciones de movimiento y de la velocidad están dadas en función del tiempo

\[ \begin{gather} x(t)=5\operatorname{sen}2t \tag{II} \end{gather} \]

\[ \begin{gather} v(t)=10\cos 2t \tag{III} \end{gather} \]

aislando el tiempo t en la ecuación (II)

\[ \begin{gather} t=\frac{1}{2}\operatorname{arcsen}\frac{x}{5} \end{gather} \]

sustituyendo este valor en la ecuación (III), obtenemos la ecuación de la velocidad en función de la posición v(x)

\[ \begin{gather} v=10\cos 2t\\[5pt] v=10\cos\left(\cancel 2\times\frac{1}{\cancel 2}\operatorname{arcsen}\frac{x}{5}\right) \end{gather} \]

\[ \begin{gather} \bbox[5px,border:5px solid #99CCFF] {v(x)=10\cos\left(\operatorname{arcsen}\frac{x}{5}\right)} \tag{IV} \end{gather} \]

Vamos a mostrar que la ecuación (IV) es igual a la ecuación (I). En la ecuación (IV), definiendo θ como

\[ \begin{gather} \theta=\operatorname{arcsen}\frac{x}{5}\\[5pt] \operatorname{sen}\theta=\frac{x}{5}\\[5pt] \operatorname{sen}\theta=\frac{\frac{x}{5}}{1} \end{gather} \]

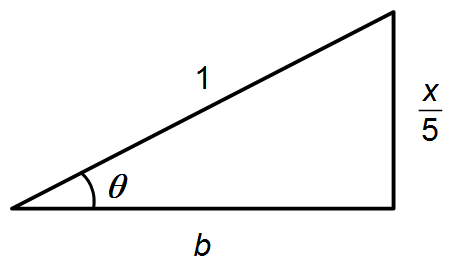
θ es el ángulo de un triángulo rectángulo con hipotenusa igual a 1 y catetos iguales a \( \left(\frac{x}{5}\right) \) y b (Figura 1).
Aplicando el Teorema de Pitágoras, encontramos el valor del cateto b

\[ \begin{gather} h^2=a^2+b^2\\[5pt] 1^2=\left(\frac{x}{5}\right)^2+b^2\\[5pt] b=\sqrt{1-\left(\frac{x}{5}\right)^2\;} \end{gather} \]

Figura 1

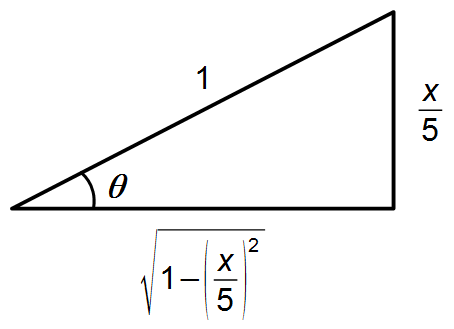
El coseno del ángulo θ está dado por (Figura 2)

\[ \begin{gather} \cos\theta=\frac{b}{1}=\frac{\sqrt{1-\left(\frac{x}{5}\right)^2\;}}{1}\\[5pt] \cos\left(\operatorname{arcsen}\frac{x}{5}\right)=\sqrt{1-\frac{x^2}{25}\;} \tag{V} \end{gather} \]

Figura 2

Sustituyendo el valor del coseno en (V) en la ecuación (IV)

\[ \begin{gather} v=10\sqrt{1-\frac{x^2}{25}\;}\\[5pt] v^2=\left(10\sqrt{1-\frac{x^2}{25}\;}\right)^2\\[5pt] v^2=100\left(1-\frac{x^2}{25}\right)\\[5pt] v^2=100\left(\frac{25-x^2}{25}\right)\\[5pt] v^2=4(25-x^2)\\[5pt] \qquad\qquad v^2=100-4x^2\qquad (:2)\\[5pt] \frac{v^2}{2}=\frac{100}{2}-\frac{4x^2}{2}\\[5pt] \frac{v^2}{2}=\frac{-{4x^2}}{2}+50 \end{gather} \]

Y la ecuación trigonométrica (IV) es igual a la ecuación algebraica (I), ambas representan el mismo sistema físico.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .