Ejercicio Resuelto sobre Campo Eléctrico
EN
FR
PT-BR
publicidad
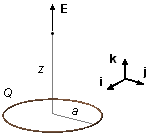
Un anillo de radio a está cargado uniformemente con una carga Q. Calcule el vector campo
eléctrico en un punto P sobre el eje de simetría perpendicular al plano del anillo a una distancia
z de su centro.
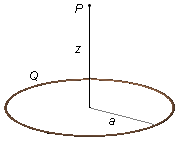
Datos del problema:
- Radio del anillo: a;
- Carga del anillo: Q;
- Distancia al punto donde se quiere el campo eléctrico: z.
El vector posición r va de un elemento de carga del anillo dq hasta el punto P donde queremos calcular el campo eléctrico, el vector rq localiza el elemento de carga en relación con el origen del referencial y el vector rp localiza el punto P (Figura 1-A).
\[
\begin{gather}
\mathbf r=\mathbf r_p-\mathbf r_q
\end{gather}
\]
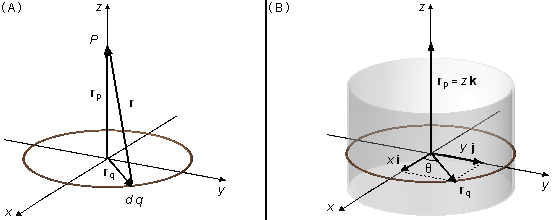
Por la geometría del problema, escogemos coordenadas cilíndricas (Figura 1-B), el vector rq, está en el plano xy, se escribe como \( \mathbf r_q=x\;\mathbf i+y\;\mathbf j \) y el vector rp solo tiene componente en la dirección k, \( \mathbf r_p=z\;\mathbf k \), el vector posición será
\[
\begin{gather}
\mathbf r=z\;\mathbf k-\left(x\;\mathbf i+y\;\mathbf j\right)\\[5pt]
\mathbf r=-x\;\mathbf i-y\;\mathbf j+z\;\mathbf k \tag{I}
\end{gather}
\]
De la ecuación (I), el módulo del vector posición r será
\[
\begin{gather}
r^2=(-x)^2+(-y)^2+z^2\\[5pt]
r=\left(x^2+y^2+z^2\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
donde x, y y z, en coordenadas cilíndricas, son dados por
\[
\begin{gather}
\left\{
\begin{array}{l}
x=a\cos\theta\\
y=a\operatorname{sen}\theta\\
z=z
\end{array}
\right. \tag{III}
\end{gather}
\]
Solución:
El vector campo eléctrico está dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{dq}{r^2}\;\frac{\mathbf r}{r}}}
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{dq}{r^3}\;\mathbf r} \tag{IV}
\end{gather}
\]
Usando la ecuación de la densidad lineal de carga λ, obtenemos el elemento de carga dq
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\end{gather}
\]
\[
\begin{gather}
dq=\lambda\;ds \tag{V}
\end{gather}
\]
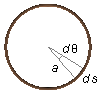
donde ds es un elemento de arco de ángulo dθ del anillo (Figura 2)
\[
\begin{gather}
ds=a\;d\theta \tag{VI}
\end{gather}
\]
sustituyendo la ecuación (VI) en la ecuación (V)
\[
\begin{gather}
dq=\lambda a\;d\theta \tag{VII}
\end{gather}
\]
Sustituyendo las ecuaciones (I), (II) y (VII) en la ecuación (IV)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[\left(x^2+y^2+z^2\right)^{1/2}\right]^3}}\left(-x\;\mathbf i-y\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left(x^2+y^2+z^2\right)^{3/2}}}\left(-x\;\mathbf i-y\;\mathbf j+z\;\mathbf k\right) \tag{VIII}
\end{gather}
\]
sustituyendo las ecuaciones de (III) en la ecuación (VIII)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[\left(a\cos\theta\right)^2+\left(a\operatorname{sen}\theta\right)^2+z^2\right]^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\operatorname{sen}\theta\;\mathbf j+z\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[a^2\cos^2\theta +a^2\operatorname{sen}^2\theta+z^2\right]^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\operatorname{sen}\theta\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[a^2\underbrace{\left(\cos^2\theta +\operatorname{sen}^2\theta\right)}_{1}+z^2\right]^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\operatorname{sen}\theta\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left(a^2+z^2\right)^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\operatorname{sen}\theta\;\mathbf j+z\;\mathbf k\;\right)
\end{gather}
\]
Como la densidad de carga λ y el radio a son constantes, pueden salir de la integral, y siendo
la integral de la suma igual a la suma de las integrales
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(a^2+z^2\right)^{3/2}}\left(-a\int\cos\theta\;d\theta\;\mathbf i-a\int\operatorname{sen}\theta\;d\theta\;\mathbf j+z\int\;d\theta\;\mathbf k\;\right)
\end{gather}
\]
Los límites de integración serán 0 y 2π (una vuelta completa en el anillo)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(a^2+z^2\right)^{3/2}}\left(-a\underbrace{\int_0^{2\pi}\cos\theta\;d\theta}_0\;\mathbf i-a\underbrace{\int_0^{2\pi}\operatorname{sen}\theta\;d\theta}_0\;\mathbf j+z\int_0^{2\pi}\;d\theta\;\mathbf k\right)
\end{gather}
\]
Integral de \( \displaystyle \int_0^{2\pi}\cos\theta\;d\theta \)
1.º método
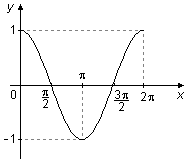Figura 3
1.º método
\[
\begin{align}
\int_0^{2\pi}\cos\theta\;d\theta &=\left.\operatorname{sen}\theta\;\right|_{\;0}^{\;2\pi}=\operatorname{sen}2\pi-\operatorname{sen}0=\\
&=0-0=0
\end{align}
\]
2.º método
El gráfico del coseno entre 0 y 2π, tiene un área “positiva” por encima del eje-x entre 0 y \( \frac{\pi}{2} \) y entre \( \frac{3\pi}{2} \) y 2π, y un área “negativa” por debajo del eje-x entre \( \frac{\pi}{2} \) y \( \frac{3\pi}{2} \), estas dos áreas se cancelan en el cálculo de la integral y el valor de la integral es cero (Figura 3).
El gráfico del coseno entre 0 y 2π, tiene un área “positiva” por encima del eje-x entre 0 y \( \frac{\pi}{2} \) y entre \( \frac{3\pi}{2} \) y 2π, y un área “negativa” por debajo del eje-x entre \( \frac{\pi}{2} \) y \( \frac{3\pi}{2} \), estas dos áreas se cancelan en el cálculo de la integral y el valor de la integral es cero (Figura 3).
Integral de \( \displaystyle \int_0^{2\pi}\operatorname{sen}\theta\;d\theta \)
1.º método
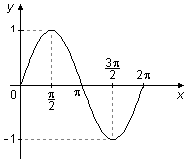Figura 4
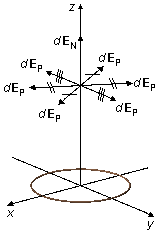Figura 5
1.º método
\[
\begin{align}
\int_0^{2\pi}\operatorname{sen}\theta\;d\theta &=\left.-\cos\theta\;\right|_{\;0}^{\;2\pi}=-(\cos 2\pi-\cos 0)=\\
&=-(1-1)=0
\end{align}
\]
2.º método
El gráfico del seno entre 0 y 2π, tiene un área “positiva” por encima del eje-x entre 0 y π y un área “negativa” por debajo del eje-x entre π y 2π, estas dos áreas se cancelan en el cálculo de la integral y el valor de la integral es cero (Figura 4).
El gráfico del seno entre 0 y 2π, tiene un área “positiva” por encima del eje-x entre 0 y π y un área “negativa” por debajo del eje-x entre π y 2π, estas dos áreas se cancelan en el cálculo de la integral y el valor de la integral es cero (Figura 4).
Observación: las dos integrales, en las direcciones i y j, siendo nulas,
representan el cálculo matemático para la afirmación que se hace usualmente de que las componentes del
campo eléctrico paralelas al plano xy (dEP) se anulan. Solo las
componentes normales al plano (dEN) contribuyen al campo eléctrico
total (Figura 5).
Integral de \( \displaystyle \int_0^{2\pi}d\theta \)
\[
\begin{gather}
\int_0^{2\pi}d\theta =\left.\theta\;\right|_{\;0}^{\;2\pi}=2\pi-0=2\pi
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(a^2+z^2\right)^{3/2}}2\pi z\;\mathbf k\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2\pi\lambda a z}{\left(a^2+z^2\right)^{3/2}}\;\mathbf k \tag{IX}
\end{gather}
\]
La carga total del anillo es Q y su longitud es 2πa, la densidad lineal de carga puede ser
escrita
\[
\begin{gather}
\lambda =\frac{Q}{2\pi a}\\[5pt]
Q=2\pi a\lambda \tag{X}
\end{gather}
\]
sustituyendo la ecuación (X) en la ecuación (IX)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{Qz}{\left(a^2+z^2\right)^{3/2}}\;\mathbf k}
\end{gather}
\]
publicidad
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .