Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad   



Un pasajero está a 5 m de distancia y corre para intentar alcanzar un tren que está partiendo del reposo con una aceleración de 2 m/s2. ¿Cuál debe ser la velocidad constante mínima del pasajero, vp, para alcanzar el tren?




Datos del problema:
  • Distancia del pasajero al tren:    d = 5 m;
  • Velocidad inicial del tren:    v0t = 0;
  • Aceleración del tren:    a = 2 m/s2.
Esquema del problema:

Este problema se puede reducir a dos puntos materiales representando al pasajero y la puerta del tren. Tomamos un sistema de referencia en el punto donde se encuentra el pasajero. La posición inicial del pasajero es S0p = 0 y la posición inicial del tren es S0t = 8 m (Figura 1).
Figura 1

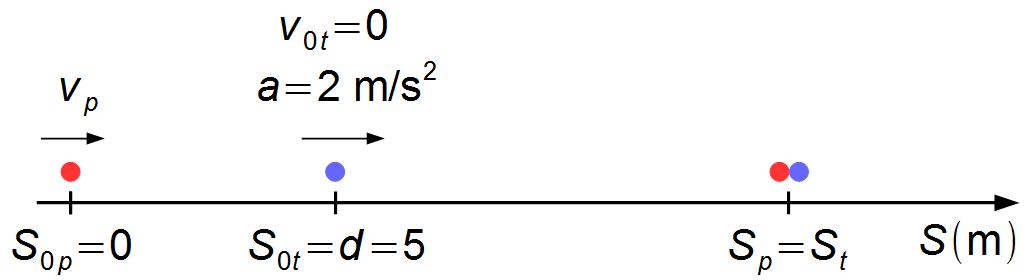
Solución

El pasajero está corriendo con velocidad constante, está en Movimiento Rectilíneo Uniforme (MRU), dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t} \end{gather} \]
\[ \begin{gather} S_p=S_{0p}+v_pt\\[5pt] S_p=0+v_pt\\[5pt] S_p=v_pt \tag{I} \end{gather} \]
El tren está con aceleración constante, está en Movimiento Rectilíneo Uniformemente Variado (MRUV), dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}t^2} \end{gather} \]
\[ \begin{gather} S_t=S_{0t}+v_{0t}+\frac{a}{2}t^2\\[5pt] S_t=5+0\times t+\frac{a}{2}t^2\\[5pt] S_t=5+t^2 \tag{II} \end{gather} \]
Para que el pasajero alcance la puerta del tren debemos imponer la condición de igualdad de las ecuaciones (I) y (II)
\[ \begin{gather} S_p=S_t\\[5pt] v_pt=5+t^2\\[5pt] t^2-v_pt+5=0 \end{gather} \]
Esta es una Ecuación de Segundo Grado en t.

Solución de la ecuación    \( t^2-v_pt+5=0 \)

\[ \begin{gather} \Delta =b^2-4ac=v_p^2-4\times 1\times 5=v_p^2-20 \end{gather} \]
\[ \begin{gather} t=\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-v_p\pm\sqrt{v_p^2-20\;}}{2\times 1} \end{gather} \]

Para que la ecuación tenga raíces reales debemos tener \( \Delta \geqslant 0\Rightarrow v_p^2-20\geqslant 0 \)
\[ \begin{gather} v_p^2-20\geqslant 0\\[5pt] v_p^2\geqslant20\\[5pt] v_p\geqslant \sqrt{20\;} \end{gather} \]
La velocidad mínima del pasajero para embarcar en el tren será
\[ \begin{gather} \bbox[#FFCCCC,10px] {v_p\simeq 4,5\;\mathrm{m/s}} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .