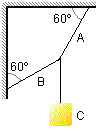
Para o sistema em equilíbrio na figura, determine as tensões nas cordas A e B sabendo que o corpo C tem 100 N.

Un montañista, con una masa de 70 kg, en cierto momento está detenido en la posición mostrada en la figura. Determinar:
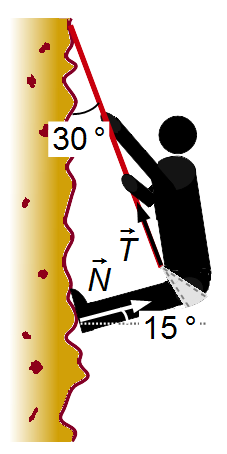
a) ¿Cuál es el módulo de la tensión en la cuerda?
b) ¿Cuál es el módulo de la fuerza normal ejercida sobre los pies del montañista?

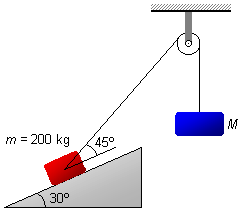
Un cuerpo, de masa 200 kg, se mantiene en equilibrio sobre un plano inclinado de 30° con respecto a la horizontal mediante una cuerda que pasa por una polea fija, y que sostiene en el otro extremo un cuerpo de masa M. La cuerda forma con la línea inclinada del plano un ángulo de 45°. Determinar:
a) La masa M;
b) La fuerza ejercida por el cuerpo contra el plano.

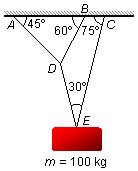
Un bloque de masa m = 100 kg está suspendido por el sistema de cuerdas mostrado en la figura. Determinar las tensiones en todas las cuerdas.
Datos: \( \operatorname{sen}15°=0,259 \), \( \cos 15°=0,966 \), \( \operatorname{sen}45°=0,707 \), \( \cos 45°=0,707 \), \( \operatorname{sen}60°=0,866 \), \( \cos 60°=0,5 \).

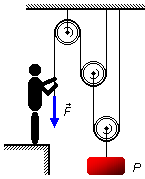
Un cuerpo con peso P está suspendido por un sistema de poleas y cuerdas. Suponiendo que estos elementos son ideales, es decir, las poleas y las cuerdas no tienen peso y no hay fricción en el sistema. Determinar:
a) La fuerza que el hombre debe ejercer en la cuerda para mantener el cuerpo en equilibrio estático;
b) Si se tira de la cuerda hacia abajo 60 cm, ¿cuánto se elevará el cuerpo?

Dos esferas idénticas, A y B, están colocadas en una caja. La línea que une el centro de las dos esferas forma un ángulo de 45° con la horizontal, y la fuerza de reacción ejercida por el fondo de la caja sobre la esfera B es de 25 N. Determinar la fuerza de reacción que la caja ejerce sobre las esferas en los puntos de contacto entre las esferas y la caja, y la fuerza que ejerce la esfera A sobre la esfera B.