Movimiento Bidimensional y Movimiento Relativo
publicidad
Movimiento Relativo
Un barco está funcionando con el motor a un régimen constante, su velocidad con respecto al agua tiene un
módulo de 5 m/s. La corriente del río se mueve con una velocidad constante de 3 m/s con respecto a la
orilla. Determine el módulo de la velocidad del barco con respecto a las orillas del río en las siguientes
situaciones:
a) El barco navega en la dirección de la corriente (río abajo);
b) El barco navega en dirección opuesta a la corriente (río arriba);
c) El barco navega en dirección perpendicular a la corriente.
a) El barco navega en la dirección de la corriente (río abajo);
b) El barco navega en dirección opuesta a la corriente (río arriba);
c) El barco navega en dirección perpendicular a la corriente.
Un barco que desarrolla una velocidad constante de 10,8 km/h desea cruzar perpendicularmente un río cuyas
aguas tienen una velocidad constante de 1,5 m/s.
a) ¿En qué dirección debería el piloto mantener el eje longitudinal del barco en relación con la normal a la corriente?
b) ¿Cuál es la velocidad del barco con respecto a la orilla del río?
a) ¿En qué dirección debería el piloto mantener el eje longitudinal del barco en relación con la normal a la corriente?
b) ¿Cuál es la velocidad del barco con respecto a la orilla del río?
En un día de lluvia sin viento, la lluvia cae verticalmente con respecto al suelo a una velocidad de 10 m/s.
Un coche se desplaza horizontalmente con una velocidad constante de 72 km/h con respecto al suelo.
a) ¿Cuál es la dirección de la lluvia con respecto al coche?
b) ¿Cuál es la velocidad de la lluvia con respecto al coche?
a) ¿Cuál es la dirección de la lluvia con respecto al coche?
b) ¿Cuál es la velocidad de la lluvia con respecto al coche?
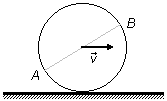
La rueda de radio R = 15 cm de la figura rueda, sin deslizarse, paralelamente a un plano vertical.
El centro C de la rueda tiene una velocidad v = 5 m/s. ¿Cuál es el módulo de la
velocidad en el punto B, en las siguientes situaciones?
a) El diámetro AB es normal al plano de rodadura;
b) El diámetro AB es paralelo al plano de rodadura.
a) El diámetro AB es normal al plano de rodadura;
b) El diámetro AB es paralelo al plano de rodadura.
Un obrero sostiene uno de los extremos de un tablón recto, de longitud a, mientras que el otro
extremo se apoya sobre un tambor cilíndrico de manera que el tablón quede en posición horizontal. Al
mover el tablón hacia adelante, el obrero hace rodar el tambor, sin deslizarse a lo largo del plano
horizontal y durante el desplazamiento el tablón permanece horizontal. Determine la distancia d
que recorrerá el obrero hasta que el extremo sostenido por él toque el tambor.

Movimiento en Dos Dimensiones
Desde el vértice de un ángulo recto parten, con un intervalo de tiempo igual a n segundos, dos
conductores, que se desplazan con velocidades constantes sobre los dos lados. Calcular las velocidades de
los dos conductores, sabiendo que después de t segundos, desde la salida del segundo conductor, su
distancia es d, y después de T segundos es D.
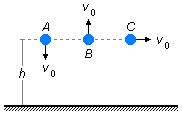
Tres esferas idénticas se lanzan desde una misma altura h con velocidades de igual magnitud. La
esfera A se lanza verticalmente hacia abajo, la B se lanza verticalmente hacia arriba y la
C se lanza horizontalmente. ¿Cuál de ellas llega al suelo con la mayor velocidad en módulo,
despreciando la resistencia del aire?
Solución por cinemática
Una pelota rueda sobre una mesa horizontal de altura H, con velocidad constante v0,
sin fricción, hasta que cae por el borde. Calcule:
a) El tiempo necesario para que la pelota alcance el suelo;
b) La distancia horizontal, desde el borde de la mesa, donde la pelota golpea el suelo;
c) La ecuación de la trayectoria del movimiento;
d) La velocidad con la que la pelota golpea el suelo.
a) El tiempo necesario para que la pelota alcance el suelo;
b) La distancia horizontal, desde el borde de la mesa, donde la pelota golpea el suelo;
c) La ecuación de la trayectoria del movimiento;
d) La velocidad con la que la pelota golpea el suelo.
Solución con referencia en el suelo apuntando hacia arriba
Solución con referencia en la tabla apuntando hacia abajo
Solución con referencia en la tabla apuntando hacia arriba
Solución con referencia en la tabla apuntando hacia abajo
Solución con referencia en la tabla apuntando hacia arriba
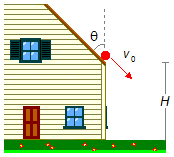
Una pelota rueda sobre el techo de una casa hasta caer por el borde con velocidad inicial
v0. La altura desde donde cae la pelota es igual a H y el ángulo de inclinación
del techo con la vertical es igual a θ. Calcula:
a) El tiempo necesario para que la pelota alcance el suelo;
b) La distancia horizontal desde la casa donde la pelota golpea el suelo;
c) La ecuación de la trayectoria del movimiento;
d) La velocidad con la que la pelota golpea el suelo.
a) El tiempo necesario para que la pelota alcance el suelo;
b) La distancia horizontal desde la casa donde la pelota golpea el suelo;
c) La ecuación de la trayectoria del movimiento;
d) La velocidad con la que la pelota golpea el suelo.
Solución con referencia en el suelo apuntando hacia arriba
Solucióncon referencia en el techo apuntando hacia abajo
Solución con referencia en el techo apuntando hacia arriba
Solucióncon referencia en el techo apuntando hacia abajo
Solución con referencia en el techo apuntando hacia arriba
Un jugador de baloncesto lanza el balón hacia la canasta desde una distancia de 4,6 m, formando un ángulo de
60° con la horizontal. La canasta está a una altura de 3,05 m y el balón está a 2,25 m del suelo cuando sale
de las manos del jugador. Calcula la velocidad inicial del balón y el tiempo que tarda el balón en ir desde
las manos del jugador hasta la canasta.
Solución con referencia en el suelo apuntando hacia arriba
Solución con referencia en las manos del jugador apuntando hacia arriba
Solución con referencia en las manos del jugador apuntando hacia arriba
Un proyectil es disparado con velocidad inicial igual a v0 y formando un ángulo
θ0 con la horizontal, sabiendo que los puntos de disparo y el objetivo están en el
mismo plano horizontal y despreciando la resistencia del aire, determine:
a) La altura máxima que alcanza el proyectil;
b) El tiempo necesario para alcanzar la altura máxima;
c) El tiempo de duración del movimiento total;
d) El alcance máximo horizontal del proyectil;
e) La ecuación de la trayectoria del movimiento del proyectil;
f) El ángulo de tiro que proporciona el máximo alcance;
g) Demostrar que los disparos con ángulos complementarios tienen el mismo alcance;
h) La velocidad en cualquier punto de la trayectoria;
i) Las componentes de la aceleración en cualquier punto de la trayectoria.
a) La altura máxima que alcanza el proyectil;
b) El tiempo necesario para alcanzar la altura máxima;
c) El tiempo de duración del movimiento total;
d) El alcance máximo horizontal del proyectil;
e) La ecuación de la trayectoria del movimiento del proyectil;
f) El ángulo de tiro que proporciona el máximo alcance;
g) Demostrar que los disparos con ángulos complementarios tienen el mismo alcance;
h) La velocidad en cualquier punto de la trayectoria;
i) Las componentes de la aceleración en cualquier punto de la trayectoria.
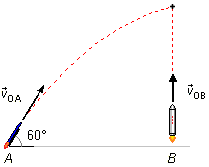
De dos puntos A y B situados a una distancia de 1000 m uno del otro, sobre un mismo plano
horizontal, se lanzan simultáneamente dos cohetes. Uno parte del punto B con una velocidad inicial
de 200 m/s dirigida de abajo hacia arriba y otro del punto A en la dirección de la vertical que
pasa por B, formando un ángulo de 60° con el horizonte. Determinar:
a) La velocidad inicial del cohete A para que intercepte al segundo;
b) Después de cuánto tiempo se produce el encuentro de los dos cohetes;
c) A qué altura se produce el encuentro;
d) Verificar si este encuentro se efectúa durante la subida o la caída del primer cohete.
a) La velocidad inicial del cohete A para que intercepte al segundo;
b) Después de cuánto tiempo se produce el encuentro de los dos cohetes;
c) A qué altura se produce el encuentro;
d) Verificar si este encuentro se efectúa durante la subida o la caída del primer cohete.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .