Ejercicio Resuelto sobre Campo Eléctrico
EN
FR
PT-BR
publicidad
Considere dos cargas iguales de mismo signo separadas por una distancia 2d. Calcule el módulo del campo eléctrico en los puntos a lo largo de la mediatriz de la línea que une las dos cargas. Verifique la solución para puntos muy alejados del centro de las cargas.
Construcción del vector de campo eléctrico resultante:
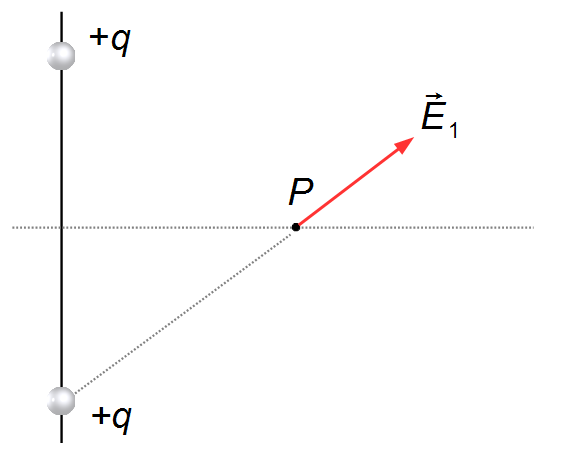
Sobre la mediatriz de la línea que conecta las cargas, elegimos un punto P cualquiera donde
queremos calcular el campo eléctrico. En la dirección del segmento de línea que conecta una de las
cargas +q al punto P, dibujamos el vector
\( \vec E_1 \)
apuntando hacia afuera de la carga, q>0 (Figura 1).
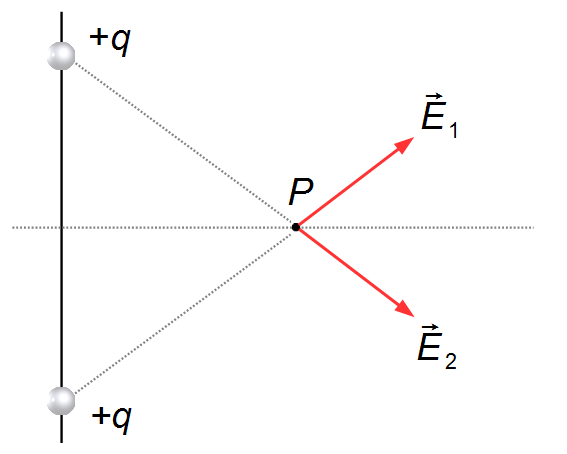
En la dirección del segmento de línea que conecta la otra carga +q al punto P, dibujamos
el vector
\( \vec E_2 \)
apuntando hacia afuera de la carga, q>0 (Figura 2).
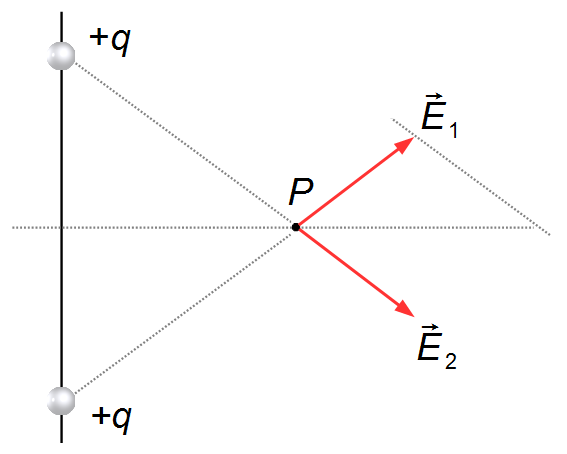
Trazamos desde el extremo del vector
\( \vec E_1 \)
una línea paralela al vector
\( \vec E_2 \)
(Figura 3).
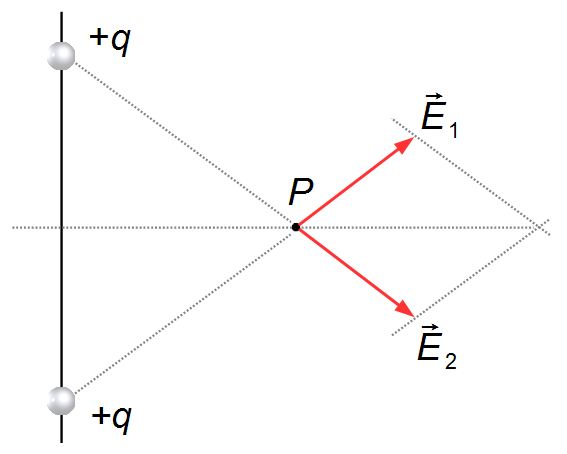
Trazamos desde el extremo del vector
\( \vec E_2 \)
una línea paralela al vector
\( \vec E_1 \)
(Figura 4).
Desde el punto P hasta la intersección de las líneas, tenemos el vector resultante
\( \vec E \),
siendo θ el ángulo entre el vector de campo eléctrico
\( \vec E_2 \)
(o el vector
\( \vec E_1 \)
) y una línea auxiliar vertical paralela a la línea que une las dos cargas. El ángulo θ que
los vectores de campo eléctrico,
\( \vec E_1 \)
y
\( \vec E_2 \),
forman con la línea auxiliar es el mismo ángulo que el segmento r forma con el segmento vertical
d (Figura 5).
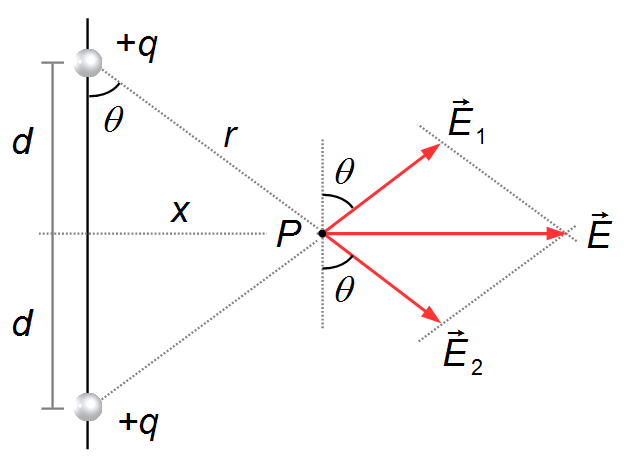
Observación 1: este sistema no representa un dipolo eléctrico, un dipolo está
formado por cargas de igual valor y signos opuestos, en este caso, tenemos cargas de igual
signo.
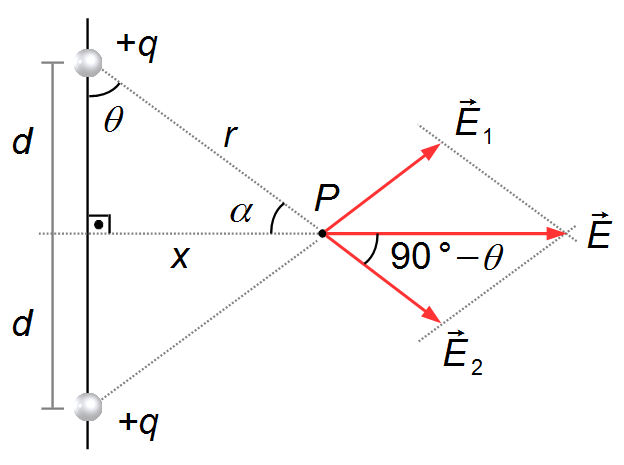Figura 6
Observación 2: en lugar de usar el ángulo θ entre el segmento r y
el segmento vertical d entre las dos cargas, podríamos usar el ángulo entre el segmento
r y el segmento x (Figura 6). La suma de los ángulos internos de un triángulo es igual
a 180°
\[
\begin{gather}
180°=90°+\theta+\alpha\\[5pt]
\alpha=90°\theta
\end{gather}
\]
Solución:
El módulo del campo eléctrico de cada carga está dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E=k_0\frac{q}{r^2}} \tag{I}
\end{gather}
\]
El campo eléctrico resultante estará dado por
\[
\begin{gather}
\vec E=\vec E_1+\vec E_2
\end{gather}
\]
como las cargas tienen el mismo valor en módulo
\( E_1=E_2 \)
\[
\begin{gather}
E=E_1\operatorname{sen}\theta+E_2\operatorname{sen}\theta\\[5pt]
E=2E_1\operatorname{sen}\theta \tag{II}
\end{gather}
\]
Observación: usando el cos 90°−θ obtenido anteriormente, el campo
eléctrico será
\[
\begin{gather}
E=2E_1\;\cos(90°-\theta)
\end{gather}
\]
el coseno de la diferencia de arcos está dado por
\[
\begin{gather}
\cos (a-b)=\cos a\cos b+\operatorname{sen}a\operatorname{sen}b\\[10pt]
\cos (90°-\theta)=\underbrace{\cos90°}_0\cos\theta+\underbrace{\operatorname{sen}90°}_1\operatorname{sen}\theta\\[5pt]
\cos(90°-\theta)=\operatorname{sen}\theta
\end{gather}
\]
El seno de θ se obtiene de r y x
\[
\begin{gather}
\operatorname{sen}\theta=\frac{x}{r} \tag{III}
\end{gather}
\]
el segmento r se obtiene usando el Teorema de Pitágoras
\[
\begin{gather}
r^2=d^2+x^2\\[5pt]
r=\sqrt{d^2+x^2\;} \tag{IV}
\end{gather}
\]
sustituyendo la ecuación (IV) en la ecuación (III)
\[
\begin{gather}
\operatorname{sen}\theta=\frac{x}{\sqrt{d^2+x^2\;}} \tag{V}
\end{gather}
\]
Sustituyendo las ecuaciones (I) y (V) en la ecuación (II)
\[
\begin{gather}
E=2k_0\frac{q}{\left(\sqrt{d^2+x^2\;}\right)^2}\frac{x}{\sqrt{d^2+x^2\;}}\\[5pt]
E=2k_0\frac{q}{\left(d^2+x^2\right)}\frac{x}{\left(d^2+x^2\right)^{\frac{1}{2}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{2k_0qx}{\left(d^2+x^2\right)^{\frac{3}{2}}}}
\end{gather}
\]
Para puntos muy alejados del centro del dipolo, tenemos x≫d, podemos despreciar el
término en d2 en el denominador y la solución será
\[
\begin{gather}
E=\frac{2k_0qx}{x^{{\cancel 2}\times{\frac{3}{\cancel 2}}}} \\[5pt]
E=\frac{2k_0q\cancel x}{x^{\cancelto{2}{3}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{2k_0q}{x^2}}
\end{gather}
\]
publicidad
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .