Ejercicios Resueltos sobre Campo Eléctrico
publicidad   



Dos cargas puntuales, de 5×10−6 C y 3×10−6 C, ocupan dos vértices de un triángulo equilátero de 1,2 m de lado. Calcular el módulo del campo eléctrico en el tercer vértice suponiendo que el medio es el vacío.


Datos del problema:
  • Carga 1:    q1 = 5×10−6 C;
  • Carga 2:    q2 = 3×10−6 C;
  • Distancia entre las cargas:    d = 1,2 m;
  • Constante de Coulomb en el vacío:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).
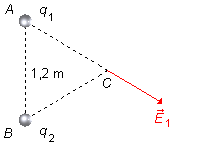
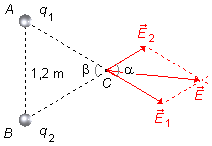
Construcción del vector campo eléctrico resultante:

Las cargas q1 y q2 están situadas en los vértices A y B del triángulo. Considerando la carga q1 de mayor valor 5×10−6 C, trazamos en el punto C el vector \( \vec E_1 \), en la dirección del segmento \( \overline{AC} \), con sentido apuntando hacia fuera de la carga, q > 0. La carga de mayor valor genera un campo más intenso (Figura 1).
Figura 1

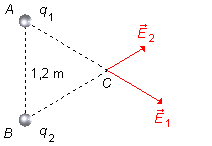
En el punto C trazamos el vector \( \vec E_2 \), en la dirección del segmento \( \overline{BC} \), con sentido hacia fuera y de tamaño menor, ya que la carga q2 es de menor valor, 3×10−6 C, y genera un campo menos intenso (Figura 2).
Figura 2

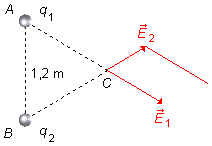
Trazamos por la extremidad del vector \( \vec E_2 \) una recta paralela al vector \( \vec E_1 \) (Figura 3).
Figura 3

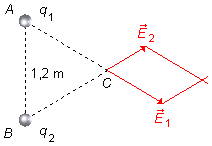
Trazamos por la extremidad del vector \( \vec E_1 \) una recta paralela al vector \( \vec E_2 \) (Figura 4).
Figura 4

Desde el vértice C hasta la intersección de las rectas tenemos el vector resultante \( \vec E \), siendo α el ángulo entre los vectores campo eléctrico \( \vec E_1 \) y \( \vec E_2 \). Como el triángulo es equilátero, todos sus ángulos internos son iguales a β = 60°. Como los ángulos α y β son opuestos por el vértice, el ángulo α también vale 60° (Figura 5).
Figura 5

Solución:

El campo eléctrico resultante, dado por
\[ \begin{gather} \vec E=\vec E_1+\vec E_2 \end{gather} \]
en módulo, puede calcularse utilizando la Ley de Cosenos
\[ \begin{gather} \bbox[#99CCFF,10px] {E^2=E_1^2+E_3^2+2E_1E_2\cos\alpha} \tag{I} \end{gather} \]
El módulo del campo eléctrico de cada carga se calcula por
\[ \begin{gather} \bbox[#99CCFF,10px] {E=k_e\frac{q}{r^2}} \end{gather} \]
\[ \begin{gather} E_1=k_e\frac{q_1}{r_1^2}\\[5pt] E_1=9\times 10^9\times \frac{5\times 10^{-6}}{(1,2)^2}\\[5pt] E_1=\frac{4,5\times 10^4}{1,44}\\[5pt] E_1\approx 3,1\times 10^4\;\mathrm{\frac{N}{C}} \tag{II} \end{gather} \]
\[ \begin{gather} E_2=k_e\frac{q_2}{r_2^2}\\[5pt] E_2=9\times 10^9\times \frac{3\times 10^{-6}}{(1,2)^2}\\[5pt] E_2=\frac{2,7\times 10^4}{1,44}\\[5pt] E_2\approx 1,9\times 10^4\;\mathrm{\frac{N}{C}} \tag{III} \end{gather} \]
sustituyendo las ecuaciones (II) y (III) en la ecuación (I).
\[ \begin{gather} E^2=(3,1\times 10^4)^2+(1,9\times 10^4)^2+2.3,1\times 10^4\times 1,9\times 10^4\cos60°\\[5pt] E^2=9,6\times 10^8+3,6\times 10^8+\cancel 2\times 5,9.10^8\times \frac{1}{\cancel 2}\\[5pt] E^2=(9,6+3,6+5,9)\times 10^8\\[5pt] E^2=19,1\times 10^8\\[5pt] E=\sqrt{19,1\times 10^8\;} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {E\approx 4,4\times 10^4\;\mathrm{\frac{N}{C}}} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .