Ejercicio Resuelto sobre Calorimetría
publicidad   



Determine el calor necesario para transformar 100 g de hielo a −10 °C en 100 g de vapor a 100 °C. También realice un gráfico de la temperatura en función de la cantidad de calor de las transformaciones. Datos:
calor específico del hielo:    ch = 0,5 cal/g°C;
calor latente de fusión:    LF = 80 cal/g;
calor específico del agua:    ca = 1,0 cal/g°C;
calor latente de vaporización:    Lv = 540 cal/g.


Datos del problema:
  • Masa de hielo:    m = 100 g;
  • Temperatura inicial del hielo:    ti = −10 °C;
  • Temperatura final del vapor:    tf = 100 °C;
  • Calor específico del hielo:    ch = 0,5 cal/g°C;
  • Calor latente de fusión:    LF = 80 cal/g;
  • Calor específico del agua:    ca = 1,0 cal/g°C;
  • Calor latente de vaporización:    Lv = 540 cal/g.
Solución:
  • 1.ª Parte
Primero, el hielo debe calentarse de −10 °C a 0 °C (Figura 1), durante esta parte no hay cambio de fase (el hielo no se convierte en agua). Usando la ecuación del calor
Figura 1
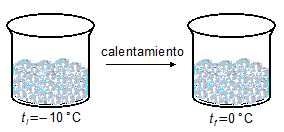
\[ \begin{gather} \bbox[#99CCFF,10px] {Q=mc\Delta t} \tag{I} \end{gather} \]
\[ \begin{gather} Q_1=mc_h\Delta t \\[5pt] Q_1=m c_h(t_0-t_{-10}) \\[5pt] Q_1=100\times 0,5\times[0-(-10)] \\[5pt] Q_1=100\times 0,5\times 10 \\[5pt] Q_1=500\;\mathrm{cal} \end{gather} \]
  • 2.ª Parte
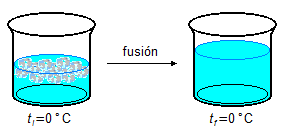
El hielo debe derretirse pasando del estado sólido al líquido, durante esta transformación, la temperatura se mantiene en 0 °C (Figura 2). Usando la ecuación para el Calor Latente
Figura 2
\[ \begin{gather} \bbox[#99CCFF,10px] {Q=mL} \tag{I} \end{gather} \]
\[ \begin{gather} Q_2=mL_F \\[5pt] Q_2=100\times 80 \\[5pt] Q_2=8000\;\mathrm{cal} \end{gather} \]
  • 3.ª Parte
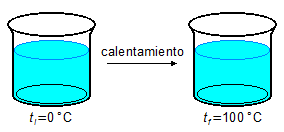
El agua debe calentarse de 0 °C a 100 °C (Figura 3), durante esta fase no hay cambio de fase (el agua no se convierte en vapor). Usando nuevamente la ecuación (I)
Figura 3
\[ \begin{gather} Q_3=m c_a\Delta t \\[5pt] Q_3=m c_a(t_{100}-t_0) \\[5pt] Q_3=100\times 1,0\times(100-0) \\[5pt] Q_3=100\times 1,0\times 100 \\[5pt] Q_3=10000\;\mathrm{cal} \end{gather} \]
  • 4.ª Parte
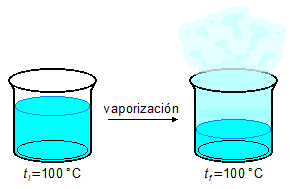
El agua debe evaporarse pasando del estado líquido al vapor, durante esta transformación, la temperatura se mantiene en 100 °C (Figura 4). Usando nuevamente la ecuación (II)
Figura 4
\[ \begin{gather} Q_4=mL_v \\[5pt] Q_4=100\times 540 \\[5pt] Q_4=54000\;\mathrm{cal} \end{gather} \]
El calor total necesario para transformar 100 g de hielo a −10°C en vapor a 100°C será la suma de todas las partes calculadas anteriormente
\[ \begin{gather} Q=Q_1+Q_2+Q_3+Q_4 \\[5pt] Q=500+8000+10000+54000 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=72500\;\mathrm{cal}} \end{gather} \]
Colocando en un gráfico los valores de las temperaturas de cada fase de las transformaciones y las cantidades de calor acumuladas en cada fase, obtenemos el gráfico de la Figura 5 a continuación

Figura 5


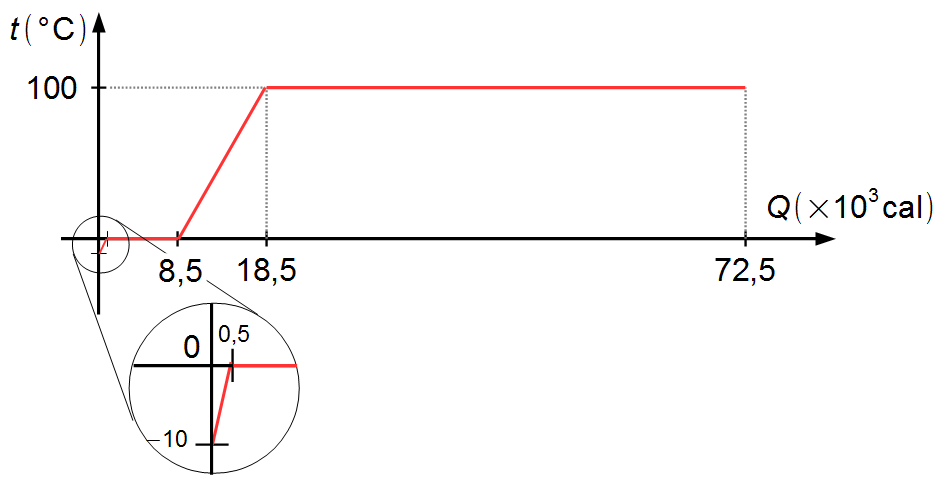
Observación: nótese que, realizado el gráfico a escala, la cantidad de calor necesaria para calentar el hielo de −10 °C a 0 °C está representada por una parte muy pequeña (mostrada en detalle), mientras que la cantidad de calor necesaria para vaporizar el agua a 100 °C ocupa la mayor parte del gráfico.
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .