Menu
FISICAEXE
Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad

Durante un neblina, un navegante recibe dos señales enviadas simultáneamente por una estación en la costa, una a través del aire y la otra a través del agua. Entre las recepciones de los dos sonidos, transcurre un intervalo de tiempo Δt=5 segundos. En las condiciones de la experiencia, la velocidad del sonido tiene los valores de 341 m/s en el aire y 1504 m/s en el agua. Determinar la distancia x entre el barco y la estación emisora de las señales.

Datos del problema:

  • Velocidad del sonido en el aire: var = 341 m/s;
  • Velocidad del sonido en el agua: vag = 1504 m/s;
  • Intervalo de tiempo entre las recepciones: Δt = 5 s.

Esquema del problema:

Dado que la onda sonora que se propaga por el agua tiene una velocidad mayor, llega primero al barco. Siendo t el tiempo de propagación de la onda en el agua, y t+Δt el tiempo de propagación de la onda en el aire (que será la suma del tiempo t de propagación en el agua con el retraso Δt que tiene por ser más lenta la propagación).

Figura 1

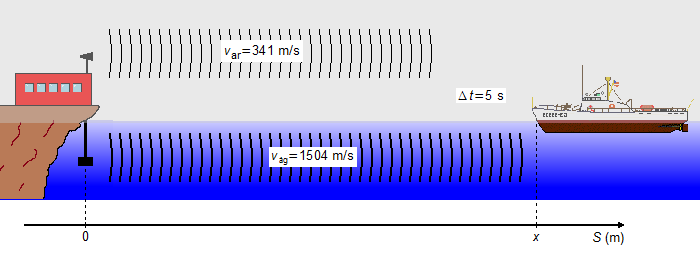
Tomamos un sistema de referencia orientado hacia la derecha con origen en la posición de emisión del sonido. La posición inicial de las ondas sonoras será S0ar = S0ag = 0, la posición del barco es x, y la posición final a donde las ondas deben llegar es Sar = Sag = x.

Solución:

Dado que las ondas tienen una velocidad constante, están en Movimiento Rectilíneo Uniforme (MRU) dado por

\[ \begin{gather} \bbox[background:#99CCFF; padding:10px; border-radius:10px;] {S=S_0+v t} \tag{I} \end{gather} \]

Aplicando la ecuación (I) para la onda que se propaga por el agua

\[ \begin{gather} S_{ag}=S_{0ag}+v_{ag}t \\[5pt] x=0+1504t \\[5pt] x=1504t \tag{II} \end{gather} \]

Aplicando la ecuación (I) para la onda que se propaga por el aire

\[ \begin{gather} S_{ar}=S_{0ar}+v_{ar}t \\[5pt] x=0+341(t+\Delta t) \\[5pt] x=341(t+5) \tag{III} \end{gather} \]

De la ecuación (II) podemos aislar el valor de t

\[ \begin{gather} t=\frac{x}{1504} \tag{IV} \end{gather} \]

sustituyendo la expresión (IV) en la ecuación (III)

\[ \begin{gather} x=341\left(\frac{x}{1504}+5\right) \\[5pt] x=\frac{341}{1504}x+341\times 5 \\[5pt] x=\frac{341}{1504}x+1705 \\[5pt] x-\frac{341}{1504}x=1705 \end{gather} \]

multiplicando ambos lados de la igualdad por 1504

\[ \begin{gather} \qquad\qquad\qquad x-\frac{341}{1504}x=1705 \qquad (\times 1504) \\[5pt] 1504 x-\cancel{1504}\times\frac{341}{\cancel{1504}}x=1705\times 1504 \\[5pt] 1163x=2564320 \\[5pt] x=\frac{2564320}{1163} \end{gather} \]
\[ \begin{gather} \bbox[background:#FFCCCC; padding:10px; border-radius:10px;] {x\approx 2205\;\mathrm m} \end{gather} \]
publicidad