Ejercicio Resuelto sobre Movimiento Circular
publicidad
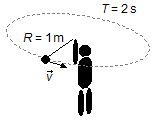
Un chico gira, sobre su cabeza, una piedra atada a un cordón con velocidad lineal constante, el radio
descrito por la circunferencia hecha por la piedra es de 1 m y da una vuelta en 2 s. Determine:
a) La velocidad lineal de la piedra;
b) El módulo de la aceleración centrípeta que actúa en la piedra.
a) La velocidad lineal de la piedra;
b) El módulo de la aceleración centrípeta que actúa en la piedra.
Datos del problema:
- Radio de la trayectoria: R = 1 m;
- Periodo de rotación: T = 2 s.
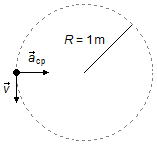
Esquema del problema:
En el sistema tenemos la velocidad \( \vec v \) que es tangente a la trayectoria, y la aceleración centrípeta \( {\vec a}_{cp} \) que actúa en la dirección del cordón, con sentido hacia el centro de la circunferencia. La aceleración centrípeta es responsable de cambiar la dirección de la velocidad lineal (hace que la piedra haga la curva).
Solución
a) La velocidad lineal está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r} \tag{I}
\end{gather}
\]
donde ω es la velocidad angular dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega=\frac{2 \pi}{T}} \tag{II}
\end{gather}
\]
sustituyendo la ecuación (II) en la ecuación (I)
\[
\begin{gather}
v=\frac{2 \pi}{T} r
\end{gather}
\]
sustituyendo los datos del problema y haciendo π = 3,14
\[
\begin{gather}
v =\frac{\cancel 2\times 3,14}{\cancel 2}\times 1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=3,14\;\mathrm{m/s}}
\end{gather}
\]
b) El módulo de la aceleración centrípeta está dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{3,14^2}{1}\\[5pt]
|\;a_{cp}\;|=\frac{9,86}{1}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{|\;a_{cp}\;|\approx 9,86\;\mathrm{m/s^2}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .