Ejercicio Resuelto sobre Mecánica de Fluidos
publicidad   



Un globo de hidrógeno con un peso de 600 N está sujeto a una cuerda en equilibrio estático vertical. Su volumen es de 80 m3 y la densidad del aire es de 1,25 kg/m3. Determine:
a) La fuerza de empuje debido al aire en el globo;
b) La fuerza de tensión en la cuerda que sostiene el globo;
c) La aceleración adquirida por el globo cuando la cuerda se rompe.
Considere constante el empuje del aire.


Datos del problema:
  • Peso del globo:    P = 600 N;
  • Volumen del globo:    Vg = 80 m3;
  • Densidad del aire:    ρar = 1,25 kg/m3;
  • Aceleración de la gravedad:    g = 9,8 m/s2.
Esquema del problema:

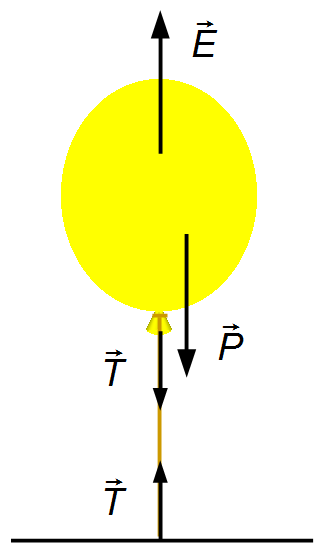
En el globo actúan la fuerza peso, \( \vec P \), la fuerza de empuje debido al aire, \( \vec E \), y la fuerza de tensión de la cuerda, \( \vec T \), que sostiene el globo (Figura 1).
Figura 1

Solución

a) La fuerza de empuje se da por
\[ \begin{gather} \bbox[#99CCFF,10px] {E=m_{\small L} g} \tag{I} \end{gather} \]
donde mL es la masa del líquido desplazado por el cuerpo, en este caso el aire, mar.
.
La densidad se da por
\[ \begin{gather} \bbox[#99CCFF,10px] {\rho=\frac{m}{V}} \end{gather} \]
con el volumen, V, del cuerpo igual al volumen de aire desplazado por el globo, Vb, y ρ es la densidad del aire, ρar
\[ \begin{gather} m_{ar}=\rho_{ar}V_g \tag{II} \end{gather} \]
sustituyendo la ecuación (II) en la ecuación (I)
\[ \begin{gather} E=\rho_{ar}V_g g\\[5pt] E=1,25\times 80\times 9,8 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {E=980\;\mathrm N} \end{gather} \]

b) Como el globo está en equilibrio estático, la resultante de las fuerzas que actúan sobre el globo es igual a cero.
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum F=0} \end{gather} \]
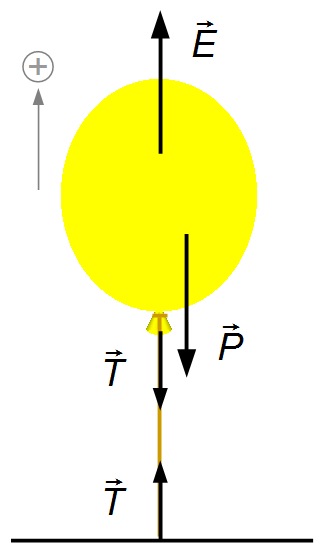
Tomando un referencial apuntado hacia arriba (Figura 2), la resultante de las fuerzas será
\[ \begin{gather} E-P-T=0\\[5pt] T=E-P\\[5pt] T=980-600 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T=380\;\mathrm N} \end{gather} \]
Figura 2

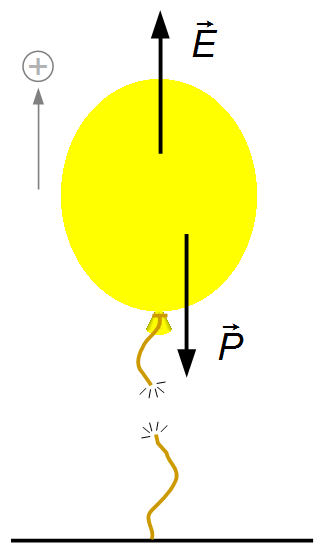
c) Cuando la cuerda se rompe, la fuerza de tensión deja de existir y el globo se mueve bajo la acción de la fuerza resultante entre el peso y la fuerza de empuje (Figura 3). Tomando un sistema de referencia orientado hacia arriba y aplicando la Segunda Ley de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
\[ \begin{gather} E-P=ma \tag{III} \end{gather} \]
El peso del globo es dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]
Figura 3

La masa del globo será
\[ \begin{gather} m=\frac{P}{g} \tag{IV} \end{gather} \]
sustituyendo la ecuación (IV) en la ecuación (III)
\[ \begin{gather} E-P=\frac{P}{g}a\\[5pt] a=(E-P)\frac{g}{P}\\[5pt] a=(980-600)\times\frac{9,8}{600}\\[5pt] \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=6,21\;\mathrm{m/s^2}} \end{gather} \]

Observación: el problema nos dice que consideremos el empuje del aire constante, lo que significa que podemos aplicar la Segunda Ley de Newton con aceleración constante. En una situación real, la densidad del aire disminuye con la altura, por lo que la fuerza de empuje también disminuye y no es constante. Cuando usamos la Segunda Ley de Newton con una fuerza variable, la aceleración ya no es constante.
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .