Solved Problem on Lagrange Equation
advertisement
An Atwood machine has masses m1 and m2
(m2 > m1) connected by an ideal rope of length ℓ of
negligible mass through a pulley of radius r with negligible mass and frictionless. Determine:
a) The acceleration of the system as a function of time;
b) The speed of the system as a function of time;
c) The equation of motion as a function of time.
a) The acceleration of the system as a function of time;
b) The speed of the system as a function of time;
c) The equation of motion as a function of time.

- Mass of block 1: m1;
- Mass of block 2: m2.
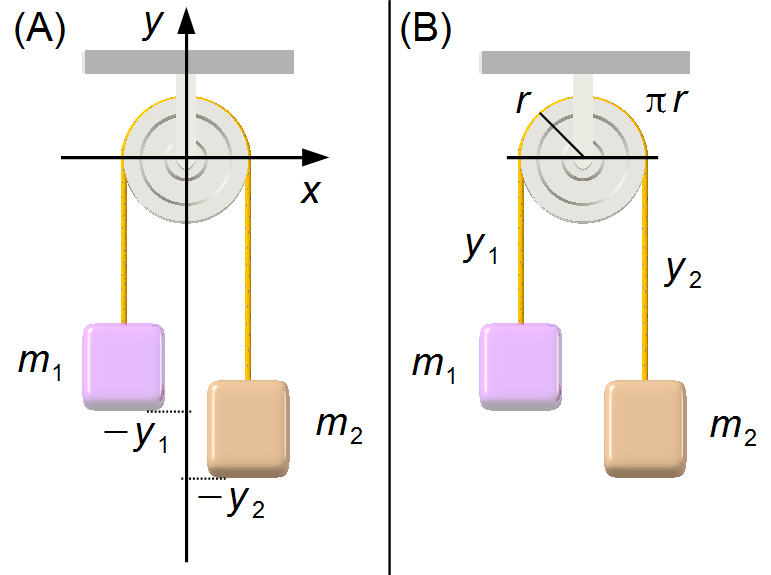
We choose a reference frame at the center of the pulley. The position of block 1 is equal to
−y1, and the position of block 2 is equal to −y2
(Figure 1-A).
The length ℓ of the rope is given by the sum of the segments y1 and y2 that support the blocks and the segment at the top of the pulley, The edge of the pulley is a circumference of radius r, its length is equal to \( \frac{C}{2}=\frac{2\pi r}{2}=\pi r \), the top is half of the circumference, \( \ell=y_{1}+y_{2}+\pi r \) (Figure 1-B). The length of the rope is given by
The length ℓ of the rope is given by the sum of the segments y1 and y2 that support the blocks and the segment at the top of the pulley, The edge of the pulley is a circumference of radius r, its length is equal to \( \frac{C}{2}=\frac{2\pi r}{2}=\pi r \), the top is half of the circumference, \( \ell=y_{1}+y_{2}+\pi r \) (Figure 1-B). The length of the rope is given by
\[
\begin{gather}
\ell=y_{1}+y_{2}+\pi r \tag{I}
\end{gather}
\]
this is an equation of constraint.
Note 1: The number of degrees of freedom of the system is f = 1. The number of
degrees of freedom is given by
In this case of the simple Atwood machine, we have N = 2, representing the two blocks.
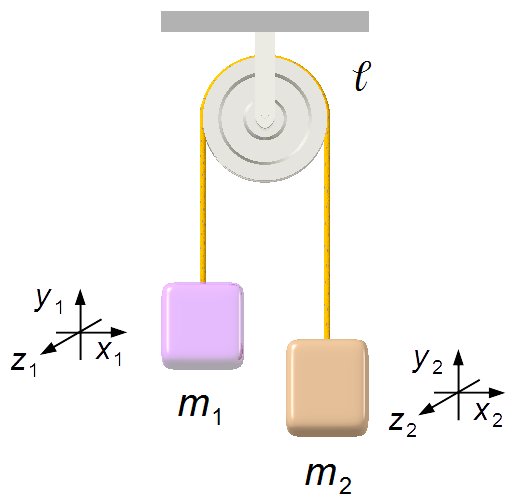 Figure 2
these four equations, together with equation (I) form a set of five constraint equations, so K = 5
and the number of degrees of freedom of the system
Figure 2
these four equations, together with equation (I) form a set of five constraint equations, so K = 5
and the number of degrees of freedom of the system
\[
\begin{gather}
f=3N-K
\end{gather}
\]
where N is the number of particles in the system, and K is the number of equations of
constaints.In this case of the simple Atwood machine, we have N = 2, representing the two blocks.
The motion of the two blocks is in the y direction, and there is no motion in the x and
z directions (Figure 2), and the equations of constraint are
\[
\begin{gather}
x_{1}=0\\[5pt]
z_{1}=0\\[5pt]
x_{2}=0\\[5pt]
z_{2}=0
\end{gather}
\]

\[
\begin{gather}
f=3\times 2-5\\[5pt]
f=1
\end{gather}
\]
Note 2: In some solutions to this problem, the equation of constraint (I) is written as
\( \ell=y_{1}+y_{2} \).
The term πr is omitted, as it is constant, and it vanishes in subsequent calculations.
Solution
a) The Lagrangian of a system is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{L=T-V} \tag{II}
\end{gather}
\]
The kinetic energy is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{T=\frac{1}{2}mv^{2}}
\end{gather}
\]
writing the kinetic energy of the two blocks
\[
\begin{gather}
T_{1}=\frac{1}{2}m_{1}{\dot{y}}_{1}^{2} \tag{III}
\end{gather}
\]
\[
\begin{gather}
T_{2}=\frac{1}{2}m_{2}{\dot{y}}_{2}^{2} \tag{IV}
\end{gather}
\]
differentiating expression (I) with respect to t
\[
\begin{gather}
\underbrace{\frac{d\left(\ell\right)}{dt}}_{0}=\frac{d\left(y_{1}\right)}{dt}+\frac{d\left(y_{2}\right)}{dt}+\underbrace{\frac{d\left(\pi r\right)}{dt}}_{0}\\[5pt]
{\dot{y}}_{1}+{\dot{y}}_{2}=0\\[5pt]
{\dot{y}}_{2}=-{\dot{y}}_{1} \tag{V}
\end{gather}
\]
since the length of the rope, ℓ, and the semicircle around the pulley, πr, are
constants, and their derivatives are equal to zero. Substituting expression (V) into expression (IV)
\[
\begin{gather}
T_{2}=\frac{1}{2}m_{2}\left(-{\dot{y}}_{1}\right)^{2}\\[5pt]
T_{2}=\frac{1}{2}m_{2}{\dot{y}}_{1}^{2} \tag{VI}
\end{gather}
\]
adding expressions (III) and (VI)
\[
\begin{gather}
T=T_{1}+T_{2}\\[5pt]
T=\frac{1}{2}m_{1}{\dot{y}}_{1}^{2}+\frac{1}{2}m_{2}{\dot{y}}_{1}^{2}\\[5pt]
T=\frac{{\dot{y}}_{1}^{2}}{2}\left(m_{1}+m_{2}\right) \tag{VII}
\end{gather}
\]
The potential energy is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{U=mgx}
\end{gather}
\]
writing the potential energy of the two blocks
\[
\begin{gather}
U_{1}=-m_{1}gy_{1} \tag{VIII}
\end{gather}
\]
\[
\begin{gather}
U_{2}=-m_{2}gy_{2} \tag{IX}
\end{gather}
\]
using expression (I), we write y2 as a function of y1
\[
\begin{gather}
y_{2}=\ell-y_{1}-\pi r \tag{X}
\end{gather}
\]
substituting expression (X) into expression (IX)
\[
\begin{gather}
U_{2}=-m_{2}g\left(\ell-y_{1}-\pi r\right) \tag{XI}
\end{gather}
\]
adding the expressions (VIII) and (XI)
\[
\begin{gather}
U=-m_{1}gy_{1}-m_{2}g\left(\ell-y_{1}-\pi r\right)\\[5pt]
U=-m_{1}gy_{1}+m_{2}gy_{1}-m_{2}g\left(\ell-\pi r\right)\\[5pt]
U=gy_{1}\left(m_{2}-m_{1}\right)-m_{2}g\left(\ell-\pi r\right) \tag{XII}
\end{gather}
\]
Substituting expressions (VII) and (XII) into expression (II)
\[
\begin{gather}
L=\frac{{\dot{y}}_{1}^{2}}{2}\left(m_{1}+m_{2}\right)-gy_{1}\left(m_{2}-m_{1}\right)+m_{2}g\left(\ell-\pi r\right)
\end{gather}
\]
since the system depends on a single variable, we write y = y1
\[
\begin{gather}
L=\frac{{\dot{y}}^{2}}{2}\left(m_{1}+m_{2}\right)-gy\left(m_{2}-m_{1}\right)+m_{2}g\left(\ell-\pi r\right) \tag{XIII}
\end{gather}
\]
The Lagrange Equation is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{d}{dt}\left(\frac{\partial L}{\partial{\dot{q}}_{j}}\right)-\frac{\partial L}{\partial q_{j}}=0} \tag{XIV}
\end{gather}
\]
we have a variable, j = 1, letting
\( q_{1}=y \)
and
\( \dot{q}_{1}=\dot{y} \)
\[
\begin{gather}
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{y}}\right)-\frac{\partial L}{\partial y}=0 \tag{XV}
\end{gather}
\]
- Differentiation of \( \displaystyle \frac{\partial L}{\partial y} \)
\[
\begin{gather}
\frac{\partial L}{\partial y}=\frac{\partial }{\partial y}\left[\frac{{\dot{y}}^{2}}{2}\left(m_{1}+m_{2}\right)-gy\left(m_{2}-m_{1}\right)+m_{2}g\left(\ell-\pi r\right)\right]\\[5pt]
\frac{\partial L}{\partial y}=\underbrace{\frac{\partial }{\partial y}\left[\frac{{\dot{y}}^{2}}{2}\left(m_{1}+m_{2}\right)\right]}_{0}-\frac{\partial}{\partial y}\left[gy\left(m_{2}-m_{1}\right)\right]+\underbrace{\frac{\partial}{\partial y}\left[m_{2}g\left(\ell-\pi r\right)\right]}_{0}\\[5pt]
\frac{\partial L}{\partial y}=-g\left(m_{2}-m_{1}\right)\\[5pt]
\frac{\partial L}{\partial y}=g\left(m_{1}-m_{2}\right)x \tag{XVI}
\end{gather}
\]
in the first and third terms, the variable y does not appear, the first term depends on
\( \dot y \),
and in the third term, all factors are constant.
- Differentiation of \( \displaystyle \frac{\partial L}{\partial \dot{y}} \)
\[
\begin{gather}
\frac{\partial L}{\partial \dot{y}}=\frac{\partial}{\partial \dot y}\left[\frac{{\dot{y}}^{2}}{2}\left(m_{1}+m_{2}\right)-gy\left(m_{1}-m_{2}\right)-m_{2}g\left(\ell-\pi r\right)\right]\\[5pt]
\frac{\partial L}{\partial \dot{y}}=\frac{\partial}{\partial \dot y}\left[\frac{{\dot{y}}^{2}}{2}\left(m_{1}+m_{2}\right)\right]-\underbrace{\frac{\partial}{\partial \dot y}\left[gy\left(m_{1}-m_{2}\right)\right]}_{0}-\underbrace{\frac{\partial}{\partial \dot y}\left[m_{2}g\left(\ell-\pi r\right)\right]}_{0}\\[5pt]
\frac{\partial L}{\partial \dot y}=\frac{\cancel{2}\dot{y}}{\cancel{2}}\left(m_{1}+m_{2}\right)\\[5pt]
\frac{\partial L}{\partial \dot y}=\dot{y}\left(m_{1}+m_{2}\right) \tag{XVIII}
\end{gather}
\]
in the second and third terms, the variable
\( \dot{y} \)
does not appear, the second term depends on y, and in the third term, all factors are constant.
- Differentiation of \( \displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right) \)
\[
\begin{gather}
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{y}}\right)=\frac{d}{dt}\left[\dot{y}\left(m_{1}+m_{2}\right)\right]\\[5pt]
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{y}}\right)=\ddot{y}\left(m_{1}+m_{2}\right) \tag{XIX}
\end{gather}
\]
Substituting expressions (XVI) and (XIX) into expression (XV)
\[
\begin{gather}
\ddot{y}\left(m_{1}+m_{2}\right)-g\left(m_{1}-m_{2}\right)=0\\[5pt]
\ddot{y}\left(m_{1}+m_{2}\right)=g\left(m_{1}-m_{2}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\ddot{y}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}}
\end{gather}
\]
b) The acceleration is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\frac{dv}{dt}}
\end{gather}
\]
writing
\( a=\ddot{y} \)
and
\( v=\dot{y} \)
\[
\begin{gather}
\ddot{y}=\frac{d\dot{y}}{dt}
\end{gather}
\]
substituting the acceleration found in the previous item in this expression
\[
\begin{gather}
\frac{d\dot{y}}{dt}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}
\end{gather}
\]
integrating both sides of the equation in dt
\[
\begin{gather}
\int \frac{d\dot{y}}{dt}\;dt=\int \frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;dt\\[5pt]
\int d\dot{y}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\int dt
\end{gather}
\]
the limits of integration are v0, the velocity at the initial instant, and
\( \dot{y} \),
the velocity at any instant in
\( d\dot{y} \),
and 0, the initial instant, and t any instant in dt
\[
\begin{gather}
\int_{v_{0}}^{\dot{y}}d\dot{y}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;\int_{0}^{t}dt\\[5pt]
\left.\dot{y}\;\right|_{\;v_{0}}^{\;\dot{y}}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\left.\;t\;\right|_{\;0}^{\;t}\\[5pt]
\dot{y}-v_{0}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\left(t-0\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\dot{y}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;t+v_{0}}
\end{gather}
\]
c) The speed is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dy}{dt}}
\end{gather}
\]
writing
\( v=\dot{y} \)
\[
\begin{gather}
\dot{y}=\frac{dy}{dt}
\end{gather}
\]
substituting the speed found in the previous item in this expression
\[
\begin{gather}
\frac{dy}{dt}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;t+v_{0}
\end{gather}
\]
integrating both sides of the equation in dt
\[
\begin{gather}
\int \frac{dy}{dt}\;dt=\int\left[\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}t+v_{0}\right]\;dt\\[5pt]
\int dy=\int \frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}t\;dt+\int v_{0}\;dt\\[5pt]
\int dy=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\int t\;dt+v_{0}\int\;dt
\end{gather}
\]
the limits of integration are y0, the position at the initial time, and y, the
position at any time in dy, and 0, the start time, and t any time in dt
\[
\begin{gather}
\int_{y_{0}}^{y}dy=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;\int_{0}^{t}t\;dt+v_{0}\;\int_{0}^{t}dt\\[5pt]
\left.y\;\right|_{\;y_{0}}^{\;y}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\left.\;\frac{t^{2}}{2}\;\right|_{\;0}^{\;t}+v_{0}\left.\;t\;\right|_{\;0}^{\;t}\\[5pt]
y-y_{0}=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;\left(\frac{t^{2}}{2}-0 \right)+v_{0}(t-0)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{y=\frac{g\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\;\frac{t^{2}}{2}+v_{0}t+y_{0}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .