Solved Problem on Contours
Português
English
advertisement
\( \mathsf{f)}\;\; \displaystyle z=t-i\sqrt{1-t^{2}\;}\qquad ,\qquad -1\leqslant t\leqslant 1 \)
The function z is a parametric function of the type
\[ \bbox[#99CCFF,10px]
{z(t)=x(t)+iy(t)}
\]
Identifying the functions x(t) and y(t)
\[
\begin{align}
& x(t)=t \tag{I}\\[10pt]
& y(t)=-\sqrt{1-t^{2}\;} \tag{II}
\end{align}
\]
substituting expression (I) into expression (II)
\[
y=-\sqrt{1-x^{2}\;}
\]
squaring both sides of equation
\[
\begin{gather}
y^{2}=\left(-\sqrt{1-x^{2}\;}\right)^{2}\\
y^{2}=1-x^{2}\\
y^{2}+x^{2}=1
\end{gather}
\]
For t = −1, we have x = −1 and
\( y=-\sqrt{1-(-1)^{2}\;}=0 \),
for t = 0, we have x = 0 and
\( y=-\sqrt{1-0^{2}\;}=-1 \),
for t = 1, we have x = 1 and
\( y=-\sqrt{1-1^{2}\;}=0 \).
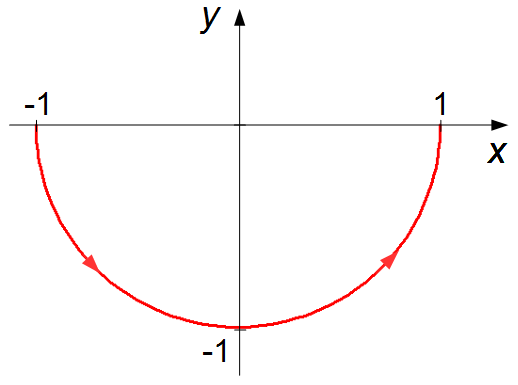
The function z(t) represents a semicircle below the x-axis and oriented from −1 to 1, (Graph 1).
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .