Solved Problem on Contours
advertisement
\( \mathsf{c)}\;\; \displaystyle z=\frac{1}{t}+it\qquad ,\qquad 1\leqslant t\lt \infty \)
The function z is a parametric function of the type
\[ \bbox[#99CCFF,10px]
{z(t)=x(t)+iy(t)}
\]
Identifying the functions x(t) and y(t)
\[
\begin{align}
& x(t)=\frac{1}{t} \tag{I}\\[10pt]
& y(t)=t \tag{II}
\end{align}
\]
substituting expression (II) into expression (I)
\[
\begin{gather}
x=\frac{1}{y}\\
y=\frac{1}{x}
\end{gather}
\]
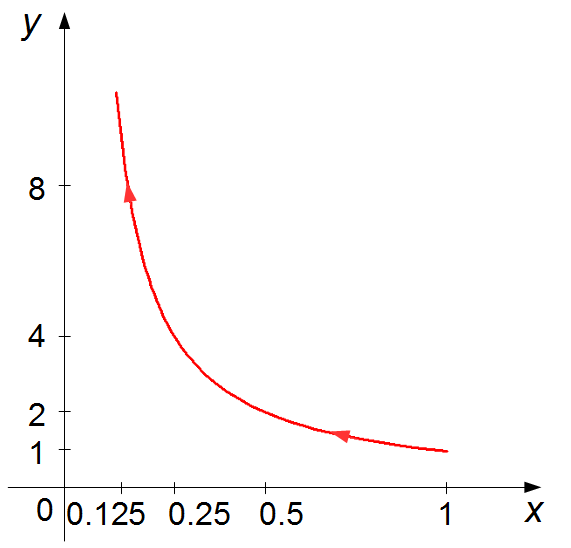
The function z(t) represents a segment of hyperbola oriented from the point (1, 1) to (0, ∞), (Graph 1).
Note: About curve orientation.
Graph 2
Graph 3
Graph 4
When the parameter t varies from 1 to infinity, the curve is traversed in the orientation that x varies from 1 and tends to 0, and y varies from 1 and tends to infinity.
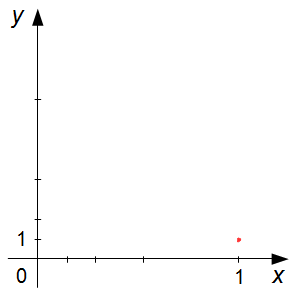
When the parameter t is equal to 1, y = t = 1, and
\( x=\frac{1}{t}=\frac{1}{1}=1 \),
we have the point (1, 1), (Graph 2).

Graph 2
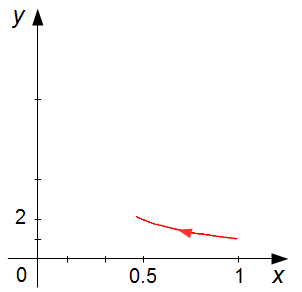
When parameter t is equal to 2, y = t = 2, and
\( x=\frac{1}{t}=\frac{1}{2}=0.5 \),
the curve is oriented towards the point (0.5; 2), (Graph 3).

Graph 3
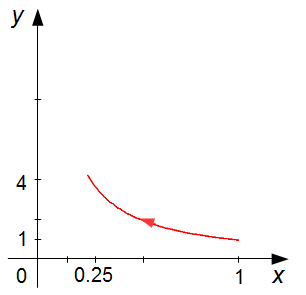
When parameter t is equal to 4, y = t = 4, and
\( x=\frac{1}{t}=\frac{1}{4}=0.25 \),
the curve is oriented towards the point (0.25; 4), (Graph 4).

Graph 4
When the parameter t varies from 1 to infinity, the curve is traversed in the orientation that x varies from 1 and tends to 0, and y varies from 1 and tends to infinity.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .