Solved Problem on Cauchy's Integral Formula
advertisement
c) \( \displaystyle \oint_{{C}}\frac{\cos z}{z}\;dz \)

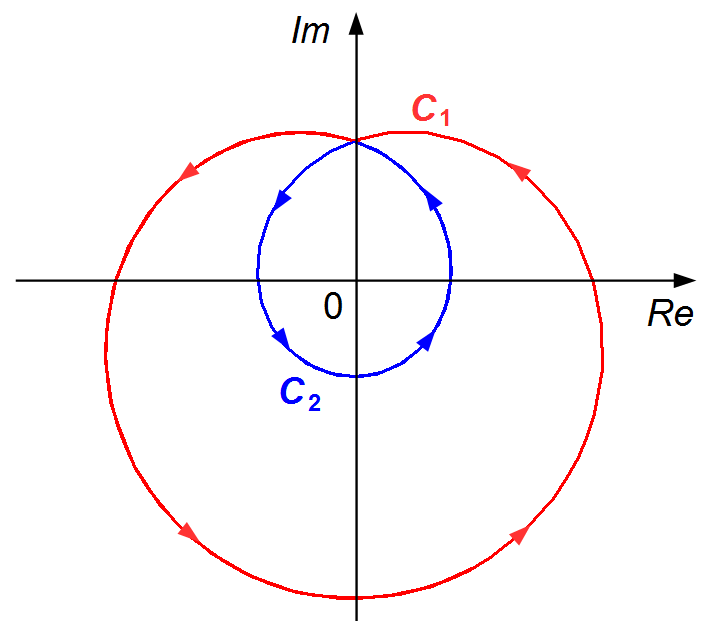
The path is given by contour C (Figure 1). We can divide contour C into two parts, an
external contour C1, traversed counterclockwise, the integration will be positive. And
an internal contour C2 traversed counterclockwise, the integration will be positive.
The point z = 0 is inside the region determined by the two contours C1 and
C2.
The integral is rewritten as
The integral is rewritten as
\[
\begin{gather}
\oint_{{C}}\frac{z}{(z+1)(z-2)}\;dz=\underbrace{\oint_{{C_{1}}}\frac{\cos z}{z}\;dz}_{I_{1}}+\underbrace{\oint_{{C_{2}}}\frac{\cos z}{z}\;dz}_{I_{2}}
\end{gather}
\]
The Cauchy Integral Formula in general form is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f^{(n)}(z_{0})=\frac{{n}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz} \tag{I}
\end{gather}
\]
dentifying the terms of the integrals.
- Integral I1:
\[
\begin{gather}
\frac{{
\bbox[#FFCC66,2px]
{n}
}!}{2\pi \mathrm{i}}\;\oint_{C}\frac{
\bbox[#FFFF66,2px]
{f(z)}
}{\left(z-
\bbox[#FFD9CC,2px]
{z_{0}}
\right)^{
\bbox[#FFCC66,2px]
{n}
+1}}\;dz=\oint_{C_{1}}\frac{
\bbox[#FFFF66,2px]
{\operatorname{cos z}}}
{\left(z-
\bbox[#FFD9CC,2px]
{0}
\right)^{
\bbox[#FFCC66,2px]
{0}
+1}}\;dz
\end{gather}
\]
we have
\( f(z)=\cos z \),
z0 = 0 and n = 0, writing the expression (I) for the integral
\[
\begin{gather}
I_{1}=\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\frac{2\pi\mathrm{i}}{n!}\;f^{(n)}(z_{0})\\[5pt]
I_{1}=\oint_{C_{1}}\frac{\cos z}{z}\;dz=\frac{2\pi \mathrm{i}}{0!}\;f^{(0)}(0)\\[5pt]
I_{1}=2\pi \mathrm{i}\cancelto{1}{\cos0}\;\\[5pt]
I_{1}=2\pi \mathrm{i} \tag{II}
\end{gather}
\]
- Integral I2:
\[
\begin{gather}
\frac{{
\bbox[#FFCC66,2px]
{n}
}!}{2\pi \mathrm{i}}\;\oint_{C}\frac{
\bbox[#FFFF66,2px]
{f(z)}
}{\left(z-
\bbox[#FFD9CC,2px]
{z_{0}}
\right)^{
\bbox[#FFCC66,2px]
{n}
+1}}\;dz=\oint_{C_{2}}\frac{
\bbox[#FFFF66,2px]
{\operatorname{cos z}}}
{\left(z-
\bbox[#FFD9CC,2px]
{0}
\right)^{
\bbox[#FFCC66,2px]
{0}
+1}}\;dz
\end{gather}
\]
we have
\( f(z)=\cos z \),
z0 = 3 and n = 0, writing the expression (I) for the integral
\[
\begin{gather}
I_{1}=\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\frac{2\pi\mathrm{i}}{n!}\;f^{(n)}(z_{0})\\[5pt]
I_{1}=\oint_{C_{2}}\frac{\cos z}{z}\;dz=\frac{2\pi \mathrm{i}}{0!}\;f^{(0)}(0)\\[5pt]
I_{1}=2\pi \mathrm{i}\cancelto{1}{\cos0}\;\\[5pt]
I_{1}=2\pi \mathrm{i} \tag{III}
\end{gather}
\]
The result of the integral will be given by the sum of the values of (II) and (III)
\[
\begin{gather}
\oint_{{C}}\frac{\cos z}{z}\;dz=I_{1}+I_{2}\\[5pt]
\oint_{{C}}\frac{\cos z}{z}\;dz=2\pi \mathrm{i}+2\pi \mathrm{i}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\oint_{{C}}\frac{\cos z}{z}\;dz=4\pi \mathrm{i}}
\end{gather}
\]
Note 1: We do not need to know the equation that describes the contour C for the
calculation, it is enough to know if the singularity points are inside or outside the region determined
by the contour.
Note 2: f(0) represents the calculation of the function at the point z0 without derivative.
Note 2: f(0) represents the calculation of the function at the point z0 without derivative.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .