Solved Problem on Harmonic Oscillations
advertisement
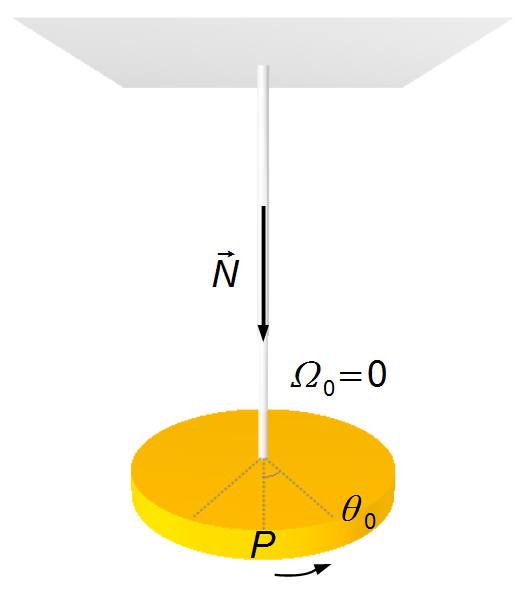
A body of mass m is suspended, by a wire of torsion constant κ, from the ceiling.
The body is displaced through an angle θ0 and released from rest. Determine:
a) The differential equation of motion;
b) The solution of the equation for the torsional pendulum and the angular frequency of oscillations;
c) The period of the oscillations.
a) The differential equation of motion;
b) The solution of the equation for the torsional pendulum and the angular frequency of oscillations;
c) The period of the oscillations.

Problem data:
- Mass of the body: m;
- Torsion constant of the wire: κ.
We choose a reference frame with a positive counter-clockwise direction. The disk is displaced and
released, the torque on the wire will make it return to the equilibrium position, and the angular
velocity will be pointing in the opposite direction of the reference frame and increasing in magnitude
towards the equilibrium position (Figure 1). With this, we write the Initial Conditions of
the problem
\[
\begin{array}{l}
\theta (0)=\theta_{0}\\[10pt]
\Omega_{0}=\dfrac{d\theta (0)}{dt}=0
\end{array}
\]
Note: For angular velocity, the symbol Ω was used to avoid confusion with
ω used for the angular frequency of oscillations.
Solution
a) Applying Newton's Second Law for rotational motion
\[
\begin{gather}
\bbox[#99CCFF,10px]
{N=I\frac{d^{2}\theta}{dt^{2}}} \tag{I}
\end{gather}
\]
the only force acting on the body is the torque on the wire
\( \vec N \)
given, in magnitude, by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{N=-\kappa \theta} \tag{II}
\end{gather}
\]
the minus sign in the torque means that it acts in the opoosite direction of the displacement
of the disk (acts in the direction of restoring the equilibrium). Substituting the expression (II into the
expression (I)
\[
\begin{gather}
-\kappa \theta =I\frac{d^{2}\theta}{dt^{2}}\\[5pt]
I\frac{d^{2}\theta}{dt^{2}}+\kappa \theta =0
\end{gather}
\]
this is a Second Order Homogeneous Differential Equation. Dividing the equation by the momento of
inertia I
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{d^{2}\theta}{dt^{2}}+\frac{\kappa}{I}\theta =0}
\end{gather}
\]
b) In the equation of the previous item we will make the following definition
\[
\begin{gather}
\omega_{0}^{2}\equiv \frac{\kappa}{I}
\end{gather}
\]
where ω0 is the angular frequency
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\omega_{0}=\sqrt{\frac{\kappa}{I}\;}}
\end{gather}
\]
\[
\begin{gather}
\frac{d^{2}\theta}{dt^{2}}+\omega_{0}^{2}\theta =0 \tag{III}
\end{gather}
\]
Solution of \( \displaystyle \frac{d^{2}\theta}{dt^{2}}+\omega_{0}^{2}\theta =0 \)
The solution to this type of equation is found substituting
The solution of the differential equation will be
Differentiation of the expression (IV) with respect to time, the function θ(t) is a composite function, using the Chain Rule
The solution to this type of equation is found substituting
\[
\begin{gather}
\theta =\operatorname{e}^{\lambda t}\hfill\\[5pt]
\frac{d\theta}{dt}=\lambda \operatorname{e}^{\lambda t}\\[5pt]
\frac{d^{2}\theta}{dt^{2}}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{gather}
\]
substituting these values into the differential equation
\[
\begin{gather}
\lambda^{2}\operatorname{e}^{\lambda t}+\omega_{0}^{2}\operatorname{e}^{\lambda t}=0\\[5pt]
\operatorname{e}^{\lambda t}\left(\lambda^{2}+\omega_{0}^{2}\right)=0\\[5pt]
\lambda^{2}+\omega_{0}^{2}=\frac{0}{\operatorname{e}^{\lambda t}}\\[5pt]
\lambda^{2}+\omega_{0}^{2}=0
\end{gather}
\]
this is the Characteristic Equation that has a solution
\[
\begin{gather}
\Delta =b^{2}-4ac=0^{2}-4 \times 1\times \omega_{0}^{2}=-4\omega_{0}^{2}\\[5pt]
\lambda_{1}=\frac{-b+\sqrt{\Delta\;}}{2a}=\frac{-0+\sqrt{-4\omega_{0}^{2}\;}}{2\times 1}=\frac{\sqrt{4\omega_{0}^{2}\;}\sqrt{-1\;}}{2}=2\omega_{0}\mathrm{i}\\[5pt]
\lambda_{2}=\frac{-b+\sqrt{\Delta \;}}{2a}=\frac{-0-\sqrt{-4\omega_{0}^{2}\;}}{2\times 1}=\frac{-\sqrt{4\omega_{0}^{2}\;}\sqrt{-1\;}}{2}=-2\omega _{0}\mathrm{i}
\end{gather}
\]
where \( \mathsf{i}=\sqrt{-1\;} \).The solution of the differential equation will be
\[
\begin{gather}
\theta =C_{1}\operatorname{e}^{\lambda_{1}t}+C_{2}\operatorname{e}^{\lambda_{2}t}\\[5pt]
\theta=C_{1}\operatorname{e}^{2\omega_{0}\mathrm{i}t}+C_{2}\operatorname{e}^{-2\omega_{0}\mathrm{i}t}
\end{gather}
\]
where C1 e C2 are constants of integration, using
Euler's Formula
\( \operatorname{e}^{\mathrm{i}\theta}=\cos \theta+\mathrm{i}\sin \theta \)
\[
\begin{gather}
\theta =C_{1}\left(\cos 2\omega_{0}t+\mathrm{i}\sin 2\omega_{0}t\right)+C_{2}\left(\cos2\omega_{0}t-\mathrm{i}\sin 2\omega_{0}t\right)\\[5pt]
\theta=C_{1}\cos 2\omega_{0}t+\mathrm{i}C_{1}\sin 2\omega_{0}t+C_{2}\cos 2\omega_{0}t-\mathrm{i}C_{2}\sin 2\omega_{0}t\\[5pt]
\theta =\left(C_{1}+C_{2}\right)\cos 2\omega_{0}t+\mathrm{i}\left(C_{1}-C_{2}\right)\sin 2\omega_{0}t
\end{gather}
\]
defining two new constants α and β in terms of C1 and
C2
\[
\begin{gather}
\alpha \equiv C_{1}+C_{2}\\[5pt]
\text{e}\\[5pt]
\beta \equiv\mathrm{i}(C_{1}-C_{2})
\end{gather}
\]
\[
\begin{gather}
\theta =\alpha \cos \omega_{0}t+\beta \sin \omega_{0}t
\end{gather}
\]
multiplying and dividing this expression by
\( \sqrt{\alpha^{2}+\beta ^{2}\;} \)
\[
\begin{gather}
\theta =\left(\alpha \cos \omega_{0}t+\beta\sin \omega_{0}t\right)\frac{\sqrt{\alpha^{2}+\beta^{2}\;}}{\sqrt{\alpha^{2}+\beta ^{2}\;}}\\[5pt]
\theta =\sqrt{\alpha^{2}+\beta ^{2}\;}\left(\frac{\alpha }{\sqrt{\alpha^{2}+\beta^{2}\;}}\cos \omega_{0}t+\frac{\beta}{\sqrt{\alpha^{2}+\beta^{2}\;}}\sin \omega_{0}t\right)
\end{gather}
\]
setting
\[
\begin{array}{l}
A\equiv \sqrt{\alpha^{2}+\beta ^{2}\;}\hfill \\[5pt]
\cos\varphi \equiv \dfrac{\alpha }{\sqrt{\alpha^{2}+\beta^{2}\;}}\\[5pt]
\sin \varphi\equiv \dfrac{\beta}{\sqrt{\alpha^{2}+\beta^{2}\;}}
\end{array}
\]
\[
\begin{gather}
\theta =A\left(\cos \varphi \cos \omega_{0}t+\sin \varphi\sin\omega_{0}t\right)
\end{gather}
\]
From the trigonometric identity
\( \cos (a-b)=\cos a\cos b-\sin a\sin b . \)
\[ \cos (a-b)=\cos a\cos b-\sin a\sin b \]
\[
\begin{gather}
\theta (t)=A\cos \left(\omega_{0}t-\varphi \right) \tag{IV}
\end{gather}
\]
where A and φ are constants determined by the Initial Conditions.Differentiation of the expression (IV) with respect to time, the function θ(t) is a composite function, using the Chain Rule
\[
\begin{gather}
\frac{d\theta [w(t)]}{dt}=\frac{d\theta}{dw}\frac{dw}{dt}
\end{gather}
\]
with
\( \theta =A\cos w \)
and
\( w=\omega_{0}t+\varphi \)
\[
\begin{gather}
\frac{d\theta}{dt}=\frac{d\theta}{dw}\frac{dw}{dt}\\[5pt]
\frac{d\theta}{dt}=\frac{d\left(A\cos w\right)}{dw}\frac{d\left(\omega_{0}t+\varphi\right)}{dt}\\[5pt]
\frac{d\theta}{dt}=A\left(-\sin w\right)\left({\omega_0}\right)\\[5pt]
\frac{d\theta}{dt}=-A\omega_{0}\sin (\omega_{0}t+\varphi) \tag{V}
\end{gather}
\]
Substituting Initial Conditions into expressions (IV) amd (V)
\[
\begin{gather}
\theta (0)=\theta_{0}=A\cos \left(\omega_{0}\times 0-\varphi\right)\\[5pt]
\theta_{0}=A\cos \varphi\\[5pt]
A=\frac{\theta_{0}}{\cos \varphi} \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{d\theta (0)}{dt}=0=-A\omega_{0}\sin (\omega _{0}\times 0+\varphi)\\[5pt]
0=-A\omega_{0}\sin \varphi \tag{VII}
\end{gather}
\]
substituting the expression (VI) into expression (VII)
\[
\begin{gather}
0=\frac{\theta_{0}}{\cos \varphi }\omega_{0}\sin \varphi\\[5pt]
\tan \varphi =0\\[5pt]
\varphi=\arctan 0\\[5pt]
\varphi=0 \tag{VIII}
\end{gather}
\]
substituting the expression (VIII) into expression (VI)
\[
\begin{gather}
A=\frac{\theta_{0}}{\cos 0}\\[5pt]
A=\theta_{0}
\end{gather}
\]
substituting the constants A and φ into expression (IV)
\[
\begin{gather}
\theta =\theta_{0}\cos \omega_{0}t
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta (t)=\theta_{0}\cos \omega_{0}t}
\end{gather}
\]
c) The period of oscillations is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{T=\frac{2\pi}{\omega}}
\end{gather}
\]
substituting the angular frequency ω0 found above
\[
\begin{gather}
T=\frac{2\pi}{\sqrt{\frac{\kappa}{I}\;}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=2\pi \sqrt{\frac{I}{\kappa}\;}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .