Solved Problem on Harmonic Oscillations
advertisement
A block of mass m is attached to a spring, the spring constant is equal to k. The block
is launched, from the equilibrium position O, with an initial velocity v0.
Determine:
a) The differential equation of motion;
b) The solution of the equation for the mass-spring system and the angular frequency of oscillations.
a) The differential equation of motion;
b) The solution of the equation for the mass-spring system and the angular frequency of oscillations.

Problem data:
- Mass of body: m;
- Spring constant: k;
- Initial position (t = 0): x0;
- Initial speed (t = 0): v0.
We choose a reference frame with a positive direction to the right. The block is at the origin of the
reference frame, x0 = 0 and launched with intial velocity v0. When
released, the spring force will act to restore the equilibrium position (Figure 1). With this, we write
the Initial Conditions of the problem
\[
\begin{align}
& x(0)=0\\[10pt]
& v=\frac{dx(0)}{dt}=v_{0}
\end{align}
\]
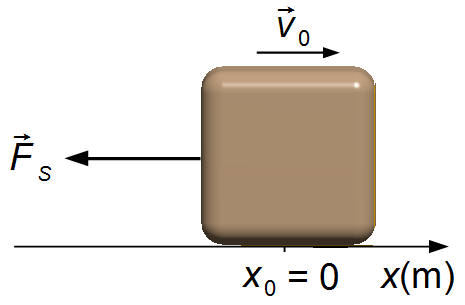
Solution
a) Applying Newton's Second Law (Figure 1)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F=m\frac{d^{2}x}{dt^{2}}} \tag{I}
\end{gather}
\]
the force acting on the block is the spring force
\( {\vec{F}}_{S} \)
given, in magnitude, by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{s}=-kx} \tag{II}
\end{gather}
\]
the minus sign in the spring force means that it acts in the opoosite direction of the displacement
of the block (acts in the direction of restoring equilibrium). Substituting the expression (II into the
expression (I)
\[
\begin{gather}
-kx=m\frac{d^{2}x}{dt^{2}}\\[5pt]
m\frac{d^{2}x}{dt^{2}}+kx=0
\end{gather}
\]
this is a Second Order Homogeneous Differential Equation. Dividing the equation by the mass m
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{d^{2}x}{dt^{2}}+\frac{k}{m}x=0}
\end{gather}
\]
b) In the equation of the previous item we will make the following definitions
\[
\begin{gather}
\omega_{0}^{2}\equiv \frac{k}{m}
\end{gather}
\]
where ω0 is the angular frequency
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\omega_{0}=\sqrt{\frac{k}{m}\;}}
\end{gather}
\]
\[
\begin{gather}
\frac{d^{2}x}{dt^{2}}+\omega_{0}^{2}x=0 \tag{III}
\end{gather}
\]
Solution of \( \displaystyle \frac{d^{2}x}{dt^{2}}+\omega_{0}^{2}x=0 \)
The solution to this type of equation is found substituting
The solution of the differential equation will be
The solution to this type of equation is found substituting
\[
\begin{array}{l}
x=\operatorname{e}^{\lambda t}\\[5pt]
\dfrac{dx}{dt}=\lambda \operatorname{e}^{\lambda t}\\[5pt]
\dfrac{d^{2}x}{dt^{2}}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{array}
\]
substituting these values into the differential equation
\[
\begin{gather}
\lambda^{2}\operatorname{e}^{\lambda t}+\omega_{0}^{2}\operatorname{e}^{\lambda t}=0\\[5pt]
\operatorname{e}^{\lambda t}\left(\lambda^{2}+\omega_{0}^{2}\right)=0\\[5pt]
\lambda^{2}+\omega_{0}^{2}=\frac{0}{\operatorname{e}^{\lambda t}}\\[5pt]
\lambda^{2}+\omega_{0}^{2}=0
\end{gather}
\]
this is the Characteristic Equation that has a solution
\[
\begin{gather}
\lambda ^{2}=-\omega_{0}^{2}\\
\lambda =\sqrt{-\omega_{0}^{2}}\\
\lambda _{1,2}=\pm \omega_{0}\text{i}
\end{gather}
\]
where \( \mathsf{i}=\sqrt{-1\;} \).The solution of the differential equation will be
\[
\begin{gather}
x=C_{1}\operatorname{e}^{\lambda_{1}t}+C_{2}\operatorname{e}^{\lambda_{2}t}\\[5pt]
x=C_{1}\operatorname{e}^{2\omega_{0}\mathsf{i}t}+C_{2}\operatorname{e}^{-2\omega_{0}\mathsf{i}t}
\end{gather}
\]
where C1 and C2 are constants of integration, using
Euler's Formula
\( \operatorname{e}^{\mathsf{i}\theta }=\cos \theta+\mathsf{i}\sin \theta \)
\[
\begin{gather}
x=C_{1}\left(\cos \omega_{0}t+\mathsf{i}\operatorname{sen}\omega_{0}t\right)+C_{2}\left(\cos\omega_{0}t-\mathsf{i}\operatorname{sen}\omega_{0}t\right)\\[5pt]
x=C_{1}\cos \omega_{0}t+\mathsf{i}C_{1}\operatorname{sen}\omega_{0}t+C_{2}\cos \omega_{0}t-\mathsf{i}C_{2}\operatorname{sen}\omega_{0}t\\[5pt]
x=\left(C_{1}+C_{2}\right)\cos \omega_{0}t+\mathsf{i}\left(C_{1}-C_{2}\right)\operatorname{sen}\omega_{0}t
\end{gather}
\]
defining two new constants α and β in terms of C1 and
C2
\[
\begin{gather}
\alpha \equiv C_{1}+C_{2}\\[5pt]
\text{and}\\[5pt]
\beta \equiv\mathsf{i}(C_{1}-C_{2})
\end{gather}
\]
\[
\begin{gather}
x=\alpha \cos \omega_{0}t+\beta \sin \omega_{0}t \tag{IV}
\end{gather}
\]
Differentiation of the expression (IV) with respect to time, the function x(t) is a sum of
functions, the derivative is given by the sum of the derivatives
\[
\begin{gather}
(f+g)'=f'+g'
\end{gather}
\]
and the functions sine and cosine are composite functions, using the Chain Rule
\[
\begin{gather}
\frac{df[w(t)]}{dt}=\frac{df}{dw}\frac{dw}{dt}
\end{gather}
\]
with
\( f=\alpha \cos w \),
\( g=\beta \sin w \)
and
\( w=\omega_{0}t \)
\[
\begin{gather}
\frac{dx}{dt}=\frac{df}{dt}+\frac{dg}{dt}\\[5pt]
\frac{dx}{dt}=\frac{df}{dw}\frac{dw}{dt}+\frac{dg}{dw}\frac{dw}{dt}\\[5pt]
\frac{dx}{dt}=\frac{d\left(\alpha\cos w\right)}{dw}\frac{d\left(\omega_{0}t\right)}{dt}+\frac{d\left(\beta\sin w\right)}{dw}\frac{d\left(\omega_{0}t\right)}{dt}\\[5pt]
\frac{dx}{dt}=\left(-\alpha\sin w\right)(\omega_{0})+\left(\beta \cos w\right)(\omega_{0})\\[5pt]
\frac{dx}{dt}=-\omega_{0}\alpha\sin \omega_{0}t+\omega_{0}\beta \cos \omega_{0}t\\[5pt]
\frac{dx}{dt}=\omega_{0}\left(-\alpha \sin \omega_{0}t+\beta \cos \omega_{0}t\right) \tag{V}
\end{gather}
\]
Substituting Initial Conditions into expressions (IV) amd (V)
\[
\begin{gather}
x(0)=0=\alpha \cancelto{1}{\cos \omega_{0}\times 0}+\beta\cancelto{0}{\sin \omega_{0}\times 0}\\[5pt]
\alpha =0 \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{dx(0)}{dt}=v_{0}=\omega_{0}\left(-\alpha\cancelto{0}{\sin \omega_{0}\times 0}+\omega_{0}\beta \cancelto{1}{\cos \omega_{0}\times 0}\right)\\
v_{0}=\omega_{0}\beta \\
\beta =\frac{v_{0}}{\omega_{0}} \tag{VII}
\end{gather}
\]
substituting the constants (VI) and (VII) into expression (IV)
\[
\begin{gather}
x=\frac{v_{0}}{\omega_{0}}\sin \omega_{0}t
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x(t)=\frac{v_{0}}{\omega_{0}}\sin \omega_{0}t}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .