Solved Problem on Coulomb's Law and Electric Field
advertisement
Determine the electric field vector of a dipole at the points located on the perpendicular bisector of the dipole. Check the answer for points far from the center of the dipole.
Problem diagram:
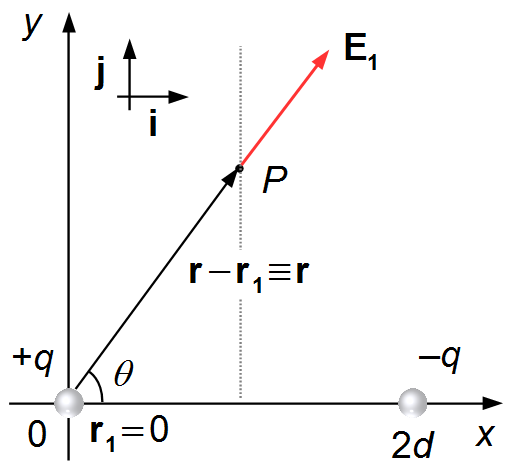
The vector r locates the point P, where we want to calculate the electric field relative
to the origin, and is written as
\( \mathbf{r}=d\;\mathbf{i}+y\;\mathbf{j} \).
The vector r1 goes from the origin to the charge +q, as the charge is located
at the origin this vector is equal to zero,
\( \mathbf{r}_{1}=\mathbf{0} \).
The vector r−r1 goes from the charge to point P, in this case it
coincides with the vector r, it is given by
\( \mathbf{\text{r}}-\mathbf{r}_{1}=d\;\mathbf{i}+y\;\mathbf{j}-\mathbf{0}=d\;\mathbf{i}+y\;\mathbf{j} \),
(Figure 1).
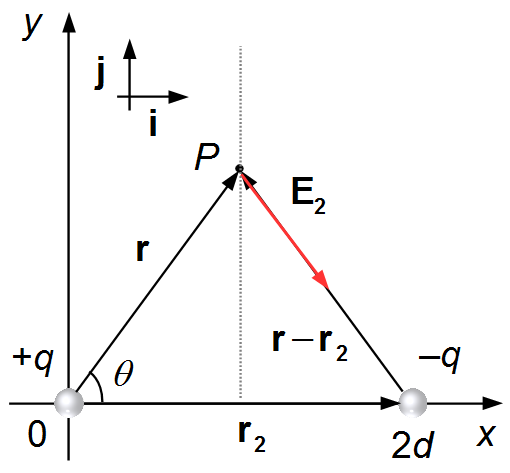
The vector r is the same as in the previous situation. The vector r2 goes from
the origin to the charge −q, and is given by
\( \mathbf{r}_{2}=2d\mathbf{i} \).
The vector r−r2 goes from the charge to the point P, and is given
by
\( \mathbf{r}-\mathbf{r}_{2}=d\;\mathbf{i}+y\;\mathbf{j}-2d\mathbf{i}=-d\;\mathbf{i}+y\;\mathbf{j} \),
(Figure 2).
Solution
The electric field vector of a discrete system of charges is calculated by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\;\sum_{i=1}^{n}\;\frac{q_{i}}{\left|\mathbf{r}-\mathbf{r}_{i}\right|^{2}}\;\frac{\mathbf{r}-\mathbf{r}_{i}}{\left|\mathbf{r}-\mathbf{r}_{i}\right|}}
\end{gather}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\left\{\frac{q_{1}}{\left|\mathbf{r}-\mathbf{r}_{1}\right|^{2}}\;\frac{\mathbf{r}-\mathbf{r}_{1}}{\left|\mathbf{r}-\mathbf{r}_{1}\right|}+\frac{q_{2}}{\left|\mathbf{r}-\mathbf{r}_{2}\right|^{2}}\;\frac{\mathbf{r}-\mathbf{r}_{2}}{\left|\mathbf{r}-\mathbf{r}_{2}\right|}\right\}
\end{gather}
\]
The denominators of the above equation are written as
\( \left|\mathbf{r}-\mathbf{r}_{1}\right|=\sqrt{d^{2}+y^{2}\;} \),
\( \left|\mathbf{r}-\mathbf{r}_{1}\right|^{2}=d^{2}+y^{2} \),
\( \left|\mathbf{r}-\mathbf{r}_{2}\right|=\sqrt{(-d)^{2}+y^{2}\;}=\sqrt{d^{2}+y^{2}\;} \).
and
\( \left|\mathbf{r}-\mathbf{r}_{2}\right|^{2}=d^{2}+y^{2} \)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\left\{\frac{q}{\left(d^{2}+y^{2}\right)^{3/2}}\;\left(d\;\mathbf{i}+y\;\mathbf{j}\right)+\frac{-q}{\left(d^{2}+y^{2}\right)^{3/2}}\;\left(-d\;\mathbf{i}+y\;\mathbf{j}\right)\right\}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{\left(d^{2}+y^{2}\right)^{3/2}}\left[d\;\mathbf{i}+y\;\mathbf{j}+d\;\mathbf{i}-y\;\mathbf{j}\right]\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{2dq}{\left(d^{2}+y^2\right)^{3/2}}\;\mathbf{i}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{2qd}{\left(d^{2}+y^{2}\right)^{3/2}}\;\mathbf{i}}
\end{gather}
\]
Note: The dipole moment p is given by the product of the charge and the distance
between them, in the result above, we have the magnitude
\[
\begin{gather}
p=q\times (2d)
\end{gather}
\]
the solution is written as
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{\left(d^{2}+y^{2}\right)^{3/2}}\;\mathbf{i}
\end{gather}
\]
For points far from the center of the dipole we have, y≫d, we can neglect the term in d2 in the denominator, and the solution will be
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{2qd}{y^{3}}\;\mathbf{i}}
\end{gather}
\]
Note: Using the dipole moment solution is written as
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{y^{3}}\;\mathbf{i}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .