Solved Problem on Electric Field
Português
English
advertisement
Determine the torque that acts on an electric dipole in a uniform electric field and determine the potential
energy of this dipole.
Problem diagram:
The dipole consists of two charges of equal magnitude and opposite signs, +q and −q, placed in an external electric field E. In the positive charge acts an electric force FE in the same direction as the electric field, and in the negative charge acts an electric force of the same magnitude and opposite direction to the electric field (Figure 1-A).
We choose a cartesian coordinate system with origin in the center of the dipole, where i, j and k are the unit vectors in directions x, y e z (Figure 1-A)
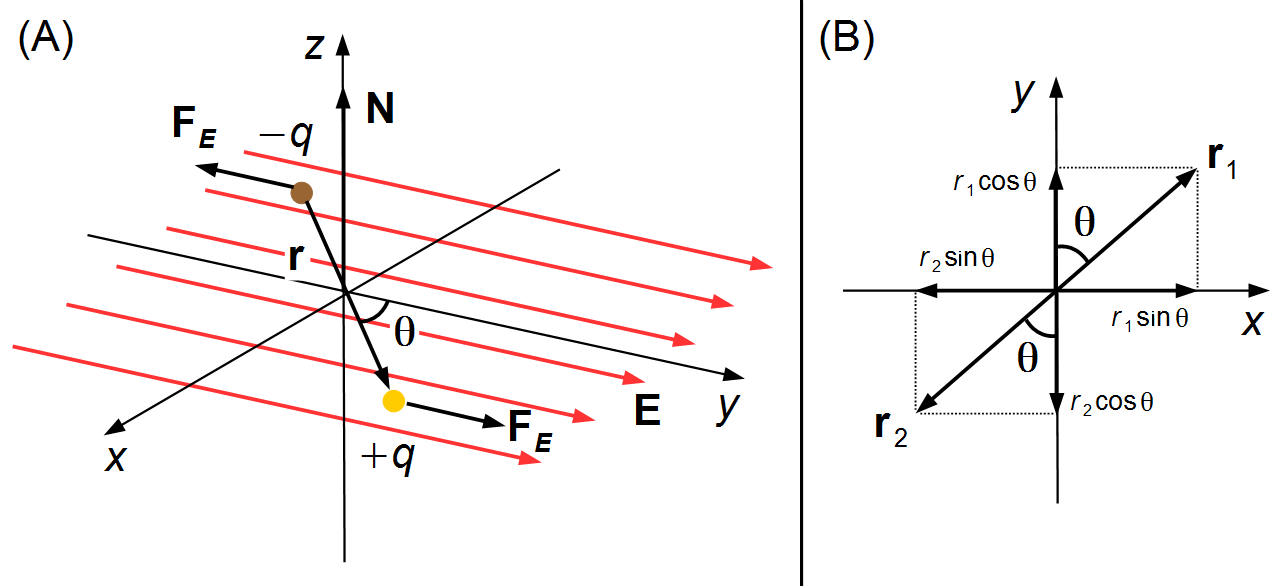Figure 1
The vector r1 locates the electric charge +q and \( r_{1}=\frac{d}{2} \), the vector r2 locates the electric charge −q and \( r_{2}=\frac{d}{2} \). The moment of dipole, is defined as pointing from the negative charge to the positive charge given by position vector r (Figures 1-A and 1-B )
Solution
Under the action of the electric force, this system rotates where torque is given by
Substituting \( \mathbf{N}=0\;\mathbf{i}+0\;\mathbf{j}+pE\sin \theta\;\mathbf{k} \) and \( d\mathbf{\theta}=0\;\mathbf{i}+0\;\mathbf{j}+d\theta\;\mathbf{k} \) into expression (VI) and calculating the dot product
The work is stored in the form of the electric potential energy in the electric field
we can write
Problem diagram:
The dipole consists of two charges of equal magnitude and opposite signs, +q and −q, placed in an external electric field E. In the positive charge acts an electric force FE in the same direction as the electric field, and in the negative charge acts an electric force of the same magnitude and opposite direction to the electric field (Figure 1-A).
We choose a cartesian coordinate system with origin in the center of the dipole, where i, j and k are the unit vectors in directions x, y e z (Figure 1-A)
The vector r1 locates the electric charge +q and \( r_{1}=\frac{d}{2} \), the vector r2 locates the electric charge −q and \( r_{2}=\frac{d}{2} \). The moment of dipole, is defined as pointing from the negative charge to the positive charge given by position vector r (Figures 1-A and 1-B )
\[
\begin{gather}
{\mathbf{r}}_{1}=r_{1}\sin \theta\;\mathbf{i}+r_{1}\cos \theta\;\mathbf{j}\\[5pt]
{\mathbf{r}}_{1}=\frac{d}{2}\sin \theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}
\end{gather}
\]
\[
\begin{gather}
{\mathbf{r}}_{2}=-r_{2}\sin \theta\;\mathbf{i}-r_{2}\cos \theta\;\mathbf{j}\\[5pt]
{\mathbf{r}}_{2}=-{\frac{d}{2}}\sin \theta\;\mathbf{i}-\frac{d}{2}\cos \theta\;\mathbf{j}
\end{gather}
\]
\[
\begin{gather}
\mathbf{r}={\mathbf{r}}_{1}-{\mathbf{r}}_{2}\\[5pt]
\mathbf{r}=\frac{d}{2}\sin \theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}-\left(-{\frac{d}{2}}\sin \theta\;\mathbf{i}-\frac{d}{2}\cos \theta\;\mathbf{j}\right)\\[5pt]
\mathbf{r}=\frac{d}{2}\sin \theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}+\frac{d}{2}\sin \theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}\\[5pt]
\mathbf{r}=d\sin \theta\;\mathbf{i}+d\cos \theta\;\mathbf{j}
\end{gather}
\]
Solution
Under the action of the electric force, this system rotates where torque is given by
\[ \bbox[#99CCFF,10px]
{\mathbf{N}=\mathbf{r}\times{\mathbf{F}}}
\]
the only force acting in the system is the electric force FE
\[
\begin{gather}
\mathbf{N}=\mathbf{r}\times{\mathbf{F}}_{E} \tag{I}
\end{gather}
\]
The electric force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{{\mathbf{F}}_{E}=q\mathbf{E}} \tag{II}
\end{gather}
\]
substituting the expression (II) into expression (I)
\[
\begin{gather}
\mathbf{N}=\mathbf{r}\times q\mathbf{E}\\
\mathbf{N}=q\mathbf{r}\times{\mathbf{E}} \tag{III}
\end{gather}
\]
The dipole moment is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{p}=q\mathbf{r}} \tag{IV}
\end{gather}
\]
substituting the expression (IV) into expression (III)
\[ \bbox[#FFCCCC,10px]
{\mathbf{N}=\mathbf{p}\times{\mathbf{E}}}
\]
The electric field is pointying in the j direction
\[
\mathbf{E}=E\;\mathbf{j}
\]
and the moment of dipole can be written as
\[
\mathbf{p}=q(d\sin \theta\;\mathbf{i}+d\cos \theta \;\mathbf{j})
\]
the torque can be written as
\[
\begin{gather}
\mathbf{p}\times{\mathbf{E}}=\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}\\
qd\sin \theta & qd\cos \theta & 0\\
0 & E &0
\end{matrix}\right|=\\[5pt]
=\left[qd\cos\theta.0-0.E\right]\;\mathbf{i}-\left[qd\sin \theta.0-0.0\right]\;\mathbf{j}+\left[qdE\sin \theta-0. qdE\right]\;\mathbf{k}\\[5pt]
\mathbf{p}\times{\mathbf{E}}=qEd\sin \theta\;\mathbf{k} \tag{V}
\end{gather}
\]
\[
\mathbf{N}=qEd\sin \theta\;\mathbf{k}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{N}=pE\sin \theta\;\mathbf{k}}
\]
The work of a force is given by
\[ \bbox[#99CCFF,10px]
{W=\int {\mathbf{F}}\cdot d\mathbf{r}}
\]
for a body spinning the force is given by the torque F = N, and the displacement is given by
the angular displacement dr = dθ
\[
\begin{gather}
W=\int {\mathbf{N}}\cdot d\mathbf{\theta } \tag{VI}
\end{gather}
\]
the vector angular displacement is given by
\[
d\mathbf{\theta }=d\theta \;\mathbf{k}
\]
Note: Some people find it difficult to understand that the vector angular displacement
points to the k direction, perpendicular to the rotation plane. When a body moves from a position
r to a position r', we have an infinitesimal ds displacement along the trajectory,
the angular displacement dθ is in the plane, but the vector angular displacement
dθ points perpendicular to the plane, this preserves the cross product (Figure 2).
The vector angular displacement indicates that the body is rotated, its magnitude indicates the angular
displacement (scalar) and the direction of the vector indicates the direction of rotation of the body,
if the vector dθ is positive, the vector product indicates that the body is if moving
clockwise, and if the vector is negative the body is moving counterclockwise.
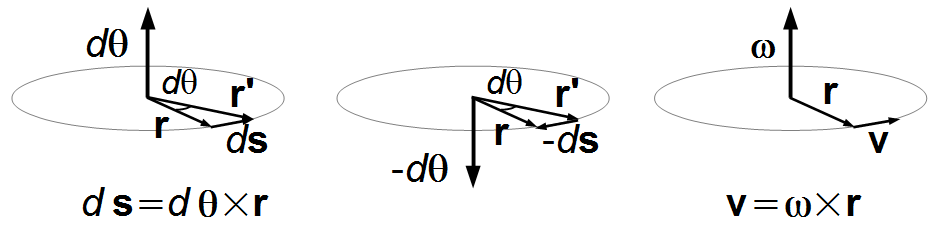Figure 2
This is the same argument used for angular velocity, the velocity v is tangent to the trajectory, but the angular velocity ω is perpendicular to the trajectory.
This is the same argument used for angular velocity, the velocity v is tangent to the trajectory, but the angular velocity ω is perpendicular to the trajectory.
Substituting \( \mathbf{N}=0\;\mathbf{i}+0\;\mathbf{j}+pE\sin \theta\;\mathbf{k} \) and \( d\mathbf{\theta}=0\;\mathbf{i}+0\;\mathbf{j}+d\theta\;\mathbf{k} \) into expression (VI) and calculating the dot product
\[
\begin{gather}
W=\int(0\;\mathbf{i}+0\;\mathbf{j}+pE\sin \theta\;\mathbf{k})\dot{\;}(0\;\mathbf{i}+0\;\mathbf{j}+d\theta\;\mathbf{k})\\[5pt]
W=\int0.0\;\underbrace{\mathbf{i}.\mathbf{i}}_{1}+0.0\;\underbrace{\mathbf{j}.\mathbf{j}}_{1}+pE\sin \theta d\theta\;\underbrace{\mathbf{k}.\mathbf{k}}_{1}\\[5pt]
W=\int pE\sin \theta \;d\theta \\W=pE\int_{\theta_{0}}^{\theta}\sin \theta \;d\theta \\[5pt]
W=pE\left.\left(-\cos \theta\right)\right|_{\;\theta _{0}}^{\;\theta }\\[5pt]
W=-pE\left(\cos \theta-\cos \theta _{0}\right)
\end{gather}
\]
Note: As i is a unit vector its magnitude is equal to 1, and the angle with the
vector itself is equal to (θ = 0), so
\( \mathbf{i}.\mathbf{i}=|\;\mathbf{i}\;|\;|\;\mathbf{i}\;|\cos0=1.1.1=1 \).
The work is stored in the form of the electric potential energy in the electric field
\[
\begin{gather}
W=\Delta U\\
\Delta U=-pE(\cos \theta -\cos \theta_{0})
\end{gather}
\]
choosing the initial situation
\( \theta_{0}=\frac{\pi}{2}\Rightarrow \cos \theta_{0}=0 \)
\[ \bbox[#FFCCCC,10px]
{U=-pE\cos \theta}
\]
Using the definition of Dot Product
\[
c=|\;a\;||\;b\;|\cos \theta
\]
\[
c=\mathbf{a}\cdot {\mathbf{b}}
\]
we can write
\[ \bbox[#FFCCCC,10px]
{U=-{\mathbf{p}}\cdot {\mathbf{E}}}
\]
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .