Solved Problem on One-dimensional Motion
advertisement   



A body is released at a height of H without air resistance. Calculate H, knowing that the body falls the last h meters in T seconds. The acceleration due to gravity is g.


Problem data:
  • Height of the fall:    H;
  • Initial position of the final part of the motion:    S0 = h;
  • Final position:    S = 0;
  • Interval of time to go through the end of the motion:    T;
  • Acceleration due to gravity:    g.
Problem diagram:

We choose a frame of reference pointing upwards, the initial position will be the height H from where the body is released, the final position will be the origin (zero), h is the height of the body when counting the final time of the fall, acceleration due to gravity and velocity will have a negative sign, they are pointing in an opposite direction of the reference frame (Figure 1).
Figure 1
Solution

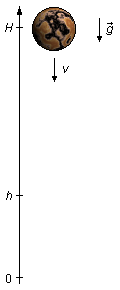
The body falls with the acceleration due to gravity, it is in free fall, given by the equation
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_{0}+v_{0} t-\frac{g}{2} t^{2}} \tag{I} \end{gather} \]
Writing the expression (I) to the final part of the motion
\[ \begin{gather} 0=h-v_{0 h}T-\frac{g}{2} T^{2} \tag{II} \end{gather} \]
where v0h indicates the initial speed does not from the initial position but from the point where the body passes through the point h.
For the calculation of v0h (Figure 2), which is the speed that the body has when falling from H to h, \( \Delta S=h-H \), from the rest, v0 = 0, as is not known the interval of time of this fall, we can use the equation of velocity as a function of displacement to get v0h
\[ \begin{gather} v^{2}=v_{0}^{2}-2g\Delta S \\ v_{0 h}^{2}=0^{2}-2g(h-H) \\ v_{0 h}=\sqrt{-2g (h-H)\;} \tag{III} \end{gather} \]
Figure 2

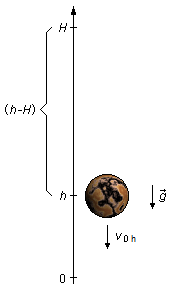
Note: Acceleration due to gravity is greater than zero, g > 0, as h < H, we have the displacement is less than zero, ΔS=h−H<0, multiplied by the factor (−2) the term within the root it is greater than zero, so there is the root.

substituting the expression (III) into expression (II)
\[ 0=h-\sqrt{-2g (h-H)\;} T-\frac{g}{2} T^{2} \]
letting the term with the square root on the left-hand side of the equation
\[ \sqrt{-2g (h-H)\;} T=h-\frac{g}{2}T^{2} \]
squaring both sides of the equation
\[ \left(\sqrt{-2g (h-H)\;} T \right)^{2}=\left(h-\frac{g}{2} T^{2} \right)^{2} \]
From the Special Binomial Products
\[ (a-b)^{2}=a^{2}-2ab+b^{2} \]

applying to the term on the right-hand side of the equation
\[ -2g (h-H) T^{2}=h^{2}-2 h \frac{g}{2} T^{2}+\frac{{g}^{2}}{4} T^{4} \]
multiplying the equation by 4
\[ \begin{gather} -4.2g (h-H) T^{2}=4h^{2}-4.2h\frac{g}{2}T^{2}+4\frac{{g}^{2}}{4}T^{4}\\ -8g (h-H) T^{2}=4h^{2}-4hgT^{2}+g^{2}T^{4} \end{gather} \]
applying the distributive property to the left-hand side of the equation
\[ \begin{gather} -8ghT^{2}+8gHT^{2}=4h^{2}-4hgT^{2}+g^{2}T^{4}\\ 8gHT^{2}=4h^{2}-4hgT^{2}+g^{2}T^{2}+8ghT^{4}\\ H=\frac{4h^{2}+4hgT^{2}+g^{2}T^{4}}{8gT^{2}} \end{gather} \]
From the Special Binomial Products
\[ (a+b)^{2}=a^{2}+2ab+b^{2} \]

at the term of the numerator, we have the following associations
\[ \begin{gather} a^{2}=4h^{2}\\ 2ab=4ghT^{2}\\ b^{2}=g^{2}T^{4} \end{gather} \]
\[ \bbox[#FFCCCC,10px] {H=\frac{(2h+gT^{2})^{2}}{8gT^{2}}} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .