Solved Problem on One-dimensional Motion

A passenger is 5 meters away and runs to try to catch a train starting from rest with an acceleration of 2 m/s². What must be the passenger's minimum constant speed, v_p, to reach the train?

Problem data:

Distance of the passenger to the train: d = 5 m;
Initial speed of the train: v_0t = 0;
Acceleration of the train: a = 2 m/s².

Problem diagram:

This problem can be reduced to two-point masses representing the passenger and the train door. We choose a reference frame at the point where the passenger is located. The initial position of the passenger is S_0p = 0 and the initial position of the train is S_0t = 8 m (Figure 1).

Figure 1

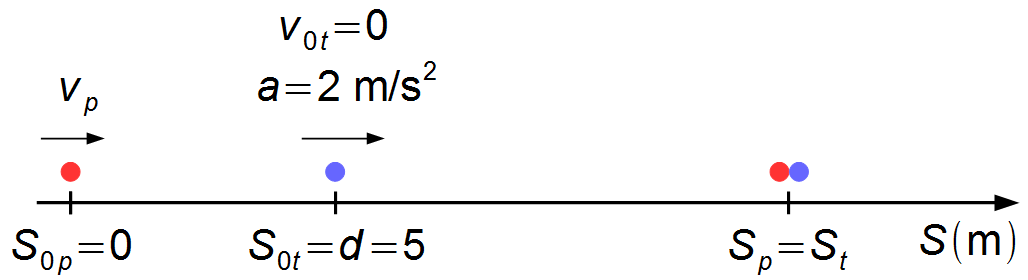
Solution

The passenger is running at a constant speed and is in Uniform Rectilinear Motion, given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t} \end{gather} \]

\[ \begin{gather} S_p=S_{0p}+v_pt\\[5pt] S_p=0\;\mathrm m+v_pt\\[5pt] S_p=v_pt \tag{I} \end{gather} \]

The train is accelerating constantly and is in Uniformly Accelerated Rectilinear Motion, given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}t^2} \end{gather} \]

\[ \begin{gather} S_t=S_{0t}+v_{0t}+\frac{a}{2}t^2\\[5pt] S_t=5\;\mathrm m+0\;\mathrm{\frac{m}{s}}\times t+\frac{a}{2}t^2\\[5pt] S_t=5\;\mathrm m+t^2 \tag{II} \end{gather} \]

For the passenger to reach the train door, we must impose the condition of equality between equations (I) and (II)

\[ \begin{gather} S_p=S_t\\[5pt] v_pt=5\;\mathrm m+t^2\\[5pt] t^2-v_pt+5\;\mathrm m=0 \end{gather} \]

This is a Quadratic Equation in t.

Solution of the equation \( t^2-v_pt+5=0 \)

\[ \begin{gather} \Delta =b^2-4ac=v_p^2-4\times 1\;\mathrm{\frac{m}{s^2}}\times 5\;\mathrm m=v_p^2-20\;\mathrm{\frac{m^2}{s^2}} \end{gather} \]

\[ \begin{gather} t=\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-v_p\pm\sqrt{v_p^2-20\;\mathrm{\frac{m^2}{s^2}}\;}}{2\times 1} \end{gather} \]

For the equation to have real roots, we must have \( \Delta \geqslant 0\Rightarrow v_p^2-20\;\mathrm{\frac{m^2}{s^2}}\geqslant 0 \)

\[ \begin{gather} v_p^2-20\;\mathrm{\frac{m^2}{s^2}}\geqslant 0\\[5pt] v_p^2\geqslant 20\;\mathrm{\frac{m^2}{s^2}}\\[5pt] v_p\geqslant \sqrt{20\;\mathrm{\frac{m^2}{s^2}}\;} \end{gather} \]

The minimum speed of the passenger to board the train will be

\[ \begin{gather} \bbox[#FFCCCC,10px] {v_p\simeq 4.5\;\mathrm{m/s}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .