Solved Problem on One-dimensional Motion
advertisement
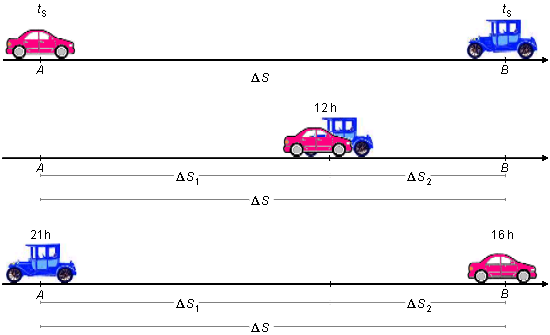
From two cities, A and B, separated by a distance ΔS, depart, at sunrise, a car from each city to another with constant speeds. At noon they meet at a point on the road, the car departed from city A reaches city B at 16 o'clock, and the car that departed from city B reaches the city at 21 o'clock. Determine at what time the sunrise.
Problem data:
- Distance between cities: ΔS;
- Instant the cars meeting: t = 12 h;
- Instant the car from A arrives at B: tAB = 16 h;
- Instant the car from B arrives at A: tBA = 21 h;
- Speed of the car that departed from the city A: vA;
- Speed of the car that departed from the city B: vB.
Solution
The total distance traveled by the cars is ΔS, dividing this distance into two parts, ΔS1 - distance traveled by car from A until the instant of the meet with the other car, and, ΔS2 - distance traveled by car from B until meet, we have \( \Delta S=\Delta S_{1}+\Delta S_{2} \). The two parts are different, because the cars are in the middle of the day (12 h), but not in the middle of the way, they leave their cities at the same time (sunrise) but arrive at different times, so their speeds are different.
The cars are moving with constant speed, in this type of motion the average speed in the route coincides with the speed of the body at any point in the trajectory, and is given by the expression of the average speed
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\bar v=\frac{\Delta S}{\Delta t}=\frac{S_{f}-S_{i}}{t_{f}-t_{i}}} \tag{I}
\end{gather}
\]
Writing the expression (I), to the car of A in the ΔS1 and
ΔS2 parts, and tS is the initial instant of the sunrise
\[
\begin{gather}
v_{A}=\frac{\Delta S_{1}}{(12-t_{S})}\\[5pt]
\Delta S_{1}=v_{A}(12-t_{S}) \tag{II}
\end{gather}
\]
\[
\begin{gather}
v_{A}=\frac{\Delta S_{2}}{(16-12)}=\frac{\Delta S_{2}}{4}\\[5pt]
\Delta S_{2}=4 v_{A} \tag{III}
\end{gather}
\]
the expressions for the car that part of B will be
\[
\begin{gather}
v_{B}=\frac{\Delta S_{2}}{(12-t_{S})}\\[5pt]
\Delta S_{2}=v_{B} (12-t_{S}) \tag{IV}
\end{gather}
\]
\[
\begin{gather}
v_{B}=\frac{\Delta S_{1}}{(21-12)}=\frac{\Delta S_{1}}{9}\\[5pt]
\Delta S_{1}=9 v_{B} \tag{V}
\end{gather}
\]
Equations (II), (III), (IV), and (V) can be written as the following system.
\[
\begin{gather}
\left\{
\begin{array}{l}
\Delta S_{2}=v_{B}(12-t_{S})\\
\Delta S_{2}=4 v_{A}\\
\Delta S_{2}=v_{B}(12-t_{S})\\
\Delta S_{1}=9 v_{B}
\end{array}
\right.
\end{gather}
\]
This system has four equations and five unknowns, ΔS1, ΔS2,
vA, vB and tS, then is an indeterminate system.As vA appears in equations (II) and (III), we can find a relationship between them by dividing two equations.
\[
\begin{gather}
\frac{\Delta S_{1}}{\Delta S_{2}}=\frac{\cancel{v_{A}}(12-t_{S})}{4\cancel{v_{A}}}\\[5pt]
4\,\Delta S_{1}=(12-t_{S})\Delta S_{2} \tag{VI}
\end{gather}
\]
Likewise, vB appears in equations (IV) and (V), dividing two equations.
\[
\begin{gather}
\frac{\Delta S_{2}}{\Delta S_{1}}=\frac{\cancel{v_{B}}(12-t_{S})}{9\cancel{v_{B}}}\\[5pt]
(12-t_{S})\Delta S_{1}=9 \Delta S_{2} \tag{VII}
\end{gather}
\]
Equations (VI) and (VII) can be written as a system of two equations.
\[
\begin{gather}
\left\{
\begin{array}{l}
4 \Delta S_{1}=(12-t_{S})\Delta S_{2}\\[5pt]
(12-t_{S})\Delta S_{1}=9 \Delta S_{2}
\end{array}
\right.
\end{gather}
\]
this system is also undetermined because it has two equations and three unknowns,
ΔS1, ΔS2 and tS, dividing equation (VI)
by (VII)
\[
\begin{gather}
\frac{4 \cancel{\Delta S_{1}}}{(12-t_{S})\cancel{\Delta S_{1}}}=\frac{(12-t_{S})\cancel{\Delta S_{2}}}{9 \cancel{\Delta S_{2}}}
\end{gather}
\]
cross multiplying
\[
\begin{gather}
4\times 9=(12-t_{S})\times(12-t_{S})\\[5pt]
36=(12-t_{S})^{2}
\end{gather}
\]
From the Special Binomial Products
\( (a-b)^{2}=a^{2}-2ab+b^{2} \)
we can write the expression on the right-hand side of the equation.
\[
\begin{gather}
36=144-24 t_{S}+t_{S}^{2}\\[5pt]
t_{S}^{2}-24t_{S}+144-36=0\\[5pt]
t_{S}^{2}-24t_{S}+108=0
\end{gather}
\]
This is a Quadratic Equation where unknown is the value tS.
Solution of the Quadratic Equation \( t_{S}^{2}-24t_{S}+108=0 \)
\[
\begin{gather}
\begin{array}{l}
\Delta=b^{2}-4ac=(-24)^{2}-4\times 1\times 108=576-432=144\\[10pt]
t=\dfrac{-b\pm\sqrt{\Delta \,}}{2a}=\dfrac{-(-24)\pm\sqrt{144\,}}{2\times 1}=\dfrac{24\pm 12}{2}
\end{array}
\end{gather}
\]
the two roots of the equation will be
\[
\begin{gather}
t_{S1}=18\;\text{h}\\[5pt]
\qquad\text{e}\qquad\\[5pt]
t_{S2}=6\;\text{h}
\end{gather}
\]
then the time of sunrise was at 6 h.
Note: The equation solution, in addition to providing the time of the sunrise request in
the problem, still gives the sunset time at 18 h.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .