Solved Problem on One-dimensional Motion
advertisement
Two trains depart simultaneously from stations P and Q. The one from P goes to Q and the one from Q goes to P on parallel lines. The first train arrives at its destination 25 minutes after having passed the second, and the second train arrives at P 49 minutes after the intersection. What is the ratio of the speed of the two trains, knowing that their speeds are constant?
Problem data:
- Time of arrival of the first train at station Q: tP = 25 minutes after crossing;
- Time of arrival of the second train at station P: tQ = 49 minutes after crossing.
Problem diagram:
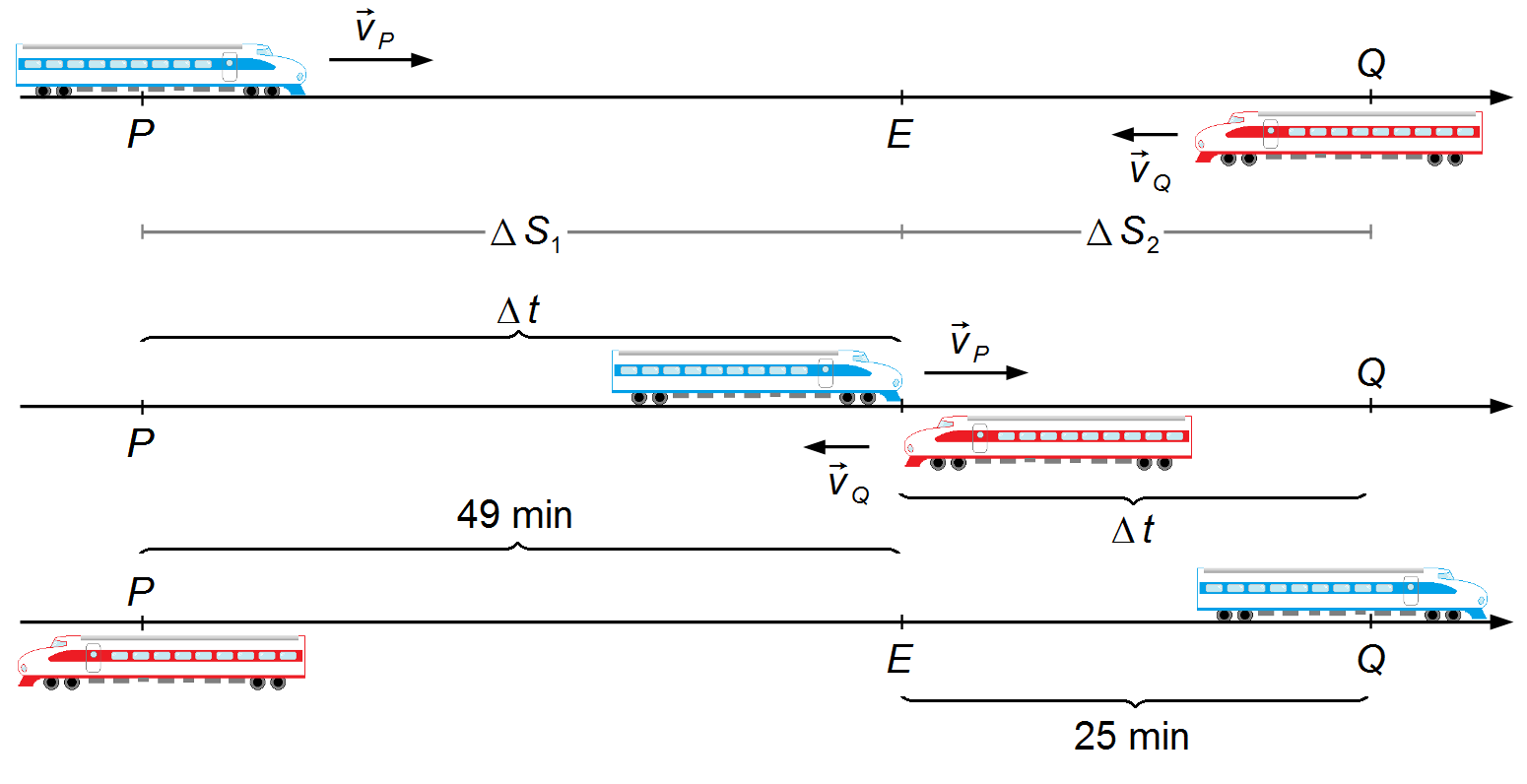
Solution
The trains are moving at constant speeds, so they are in Uniform Rectilinear Motion. In this type of motion average speed on the path coincides with the speed of the body at any point on the trajectory, and is given by the formula of the average speed
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\bar v=\frac{\Delta S}{\Delta t}} \tag{I}
\end{gather}
\]
Writing expression (I) for the train leaving P, in the intervals ΔS1 and
ΔS2, and Δt the time interval from the train leaving the station to
the point E where the trains cross
\[
\begin{gather}
v_{\small P}=\frac{\Delta S_{1}}{\Delta t} \tag{II}
\end{gather}
\]
\[
\begin{gather}
v_{\small P}=\frac{\Delta S_{2}}{25} \tag{III}
\end{gather}
\]
the expressions for the train leaving Q will be
\[
\begin{gather}
v_{\small Q}=\frac{\Delta S_{2}}{\Delta t} \tag{IV}
\end{gather}
\]
\[
\begin{gather}
v_{\small Q}=\frac{\Delta S_{1}}{49} \tag{V}
\end{gather}
\]
Equations (II), (III), (IV), and (V) can be written as a system of linear equations
\[
\begin{gather}
\left\{
\begin{matrix}
\;\Delta S_{1}=v_{\small P}\Delta t\\[5pt]
\;\Delta S_{2}=25v_{\small P}\\[5pt]
\;\Delta S_{2}=v_{\small Q}\Delta t\\[5pt]
\;\Delta S_{1}=49v_{\small Q}
\end{matrix}
\right.
\end{gather}
\]
this system has four equations and five unknowns (ΔS1,
ΔS2, vP, vQ and Δt), so it is an
indeterminate system.Dividing the first equation of the system by the fourth equation and the second by the third equation, we eliminate the terms ΔS1 and ΔS2
\[
\begin{gather}
\frac{\Delta S_{1}}{\Delta S_{1}}=\frac{v_{\small P}\Delta t}{49v_{\small Q}}\\[5pt]
1=\frac{v_{\small P}\Delta t}{49v_{\small Q}}\\[5pt]
\frac{v_{\small P}}{v_{\small Q}}=\frac{49}{\Delta t} \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{\Delta S_{2}}{\Delta S_{2}}=\frac{25v_{\small P}}{v_{\small Q}\Delta t}\\[5pt]
1=\frac{25v_{\small P}}{v_{\small Q}\Delta t}\\[5pt]
\frac{v_{\small P}}{v_{\small Q}}=\frac{\Delta t}{25} \tag{VII}
\end{gather}
\]
equating relations (VI) and (VII)
\[
\begin{gather}
\frac{49}{\Delta t}=\frac{\Delta t}{25}\\[5pt]
49\times 25=\Delta t^{2}\\[5pt]
\Delta t=\sqrt{49\times 25}
\end{gather}
\]
Using the identity of radicals
\( \sqrt[{n}]{a\times b}=\sqrt[{n}]{a}\times\sqrt[{n}]{b} \)
\[
\begin{gather}
\Delta t=\sqrt{49}.\sqrt{25}\\[5pt]
\Delta t=7\times 5\\[5pt]
\Delta t=35\;\text{min}
\end{gather}
\]
this is the time interval that trains take from departing stations P and Q to the point where
they intersect. Substituting this time interval in relation (VI)
\[
\begin{gather}
\frac{v_{\small P}}{v_{\small Q}}=\frac{49}{35}
\end{gather}
\]
dividing the numerator and denominator by 7
\[
\begin{gather}
\frac{v_{\small P}}{v_{\small Q}}=\frac{49:7}{35:7}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{v_{\small P}}{v_{\small Q}}=\frac{7}{5}}
\end{gather}
\]
Note: We could substitute the time interval Δt in relation (VII) would give
the same result.
\[
\begin{gather}
\frac{v_{\small P}}{v_{\small Q}}=\frac{35}{25}
\end{gather}
\]
dividing the numerator and denominator by 5
\[
\begin{gather}
\frac{v_{\small P}}{v_{\small Q}}=\frac{35:5}{25:5}\\[5pt]
\frac{v_{\small P}}{v_{\small Q}}=\frac{7}{5}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .