Solved Problem on One-dimensional Motion
advertisement
Two tractors start together, maneuvering in a straight line, at a construction site. The graph of velocity versus time which represents the movement of the tractors is shown in the figure. Calculate the distance that separates them at the end of the maneuver.
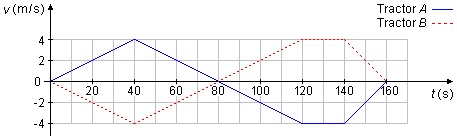
Solution
In a velocity-time graph, v = f(t), the area under the curve is equal to the displacement of the body at that time interval.
- Tractor A:
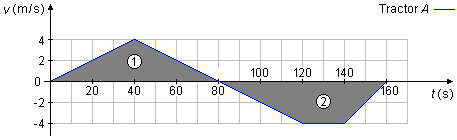
In Figure 1, the displacement of tractor A will be the sum of the area of triangle 1 with the area of trapezoid 2. The area of a triangle is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A=\frac{b h}{2}} \tag{I}
\end{gather}
\]
substituting the values from the graph in the expression (I)
\[
\begin{gather}
A=S_{1}=\frac{80\times 4}{2}\\
S_{1}=\frac{320}{2}\\
S_{1}=160\;\text{m}
\end{gather}
\]
The area of a trapezoid is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A=\frac{(B+b) h}{2}} \tag{II}
\end{gather}
\]
substituting the values from the graph in the expression (II)
\[
\begin{gather}
A=S_{2}=\frac{[(160-80)+(140-120)]\times (-4)}{2}\\
S_{2}=\frac{[80+20]\times (-4)}{2}\\
S_{2}=\frac{100\times (-4)}{2}\\
S_{2}=\frac{-400}{2}\\
S_{2}=-200\;\text{m}
\end{gather}
\]
As there is no negative area, the signal in area S2 indicates that tractor A has
moved in the opposite direction of the reference frame, position of tractor A will be
\[
\begin{gather}
S_{A}=S_{1}+S_{2}\\
S_{A}=160+(-200)\\
S_{A}=-40\;\text{m}
\end{gather}
\]
- Tractor B:
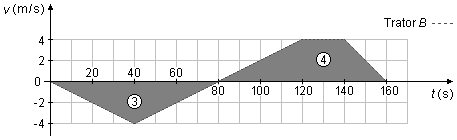
In Figure 2, the displacement of tractor B will be the sum of the area of triangle 3 with the area of trapeze 4.
substituting the values from the graph in the expression (I)
\[
\begin{gather}
A=S_{1}=\frac{80\times (-4)}{2}\\
S_{1}=\frac{-320}{2}\\
S_{1}=-160\;\text{m}
\end{gather}
\]
substituting the values from the graph in the expression (II)
\[
\begin{gather}
A=S_{2}=\frac{[(160-80)+(140-120)]\times 4}{2}\\
S_{2}=\frac{[80+20]\times 4}{2}\\
S_{2}=\frac{100\times 4}{2}\\
S_{2}=\frac{400}{2}\\
S_{2}=200\;\text{m}
\end{gather}
\]
As there is no negative area, the signal in area S3 indicates that tractor B has
moved in the opposite direction of the reference frame, position of tractor B will be
\[
\begin{gather}
S_{B}=S_{3}+S_{4}\\
S_{B}=-160+200\\
S_{B}=40\;\text{m}
\end{gather}
\]
The distance between the tractors at the end of the maneuver will be the difference in displacements
\[
\begin{gather}
\Delta S=\left|S_{A}-S_{B}\right|\\
\Delta S=\left|40-40\right|\\
\Delta S=\left|-80\right|
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\Delta S=80\;\text{m}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .