Solved Problem on Impulse and Linear Momentum

Solved Problem on Impulse

A body of mass m falls from a height H from rest, and another body of unknown mass also falls, from rest, from a height h. Calculate the mass of the unknown body such that both strike the ground with the same impulse.

Problem data:

Mass of body A: m;
Height of fall of body A: H;
Initial speed of body A: v_0A = 0;
Height of fall of body B: h;
Initial speed of body B: v_0B = 0.

Problem diagram:

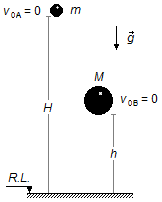
We choose M > m and H > h, both heights are measured from the ground, chosen as Reference Level (R.L.), Figure 1.

Figure 1

Solution

Using the Impulse-Momentum Theorem

\[ \begin{gather} \bbox[#99CCFF,10px] {I=\Delta Q=Q_{f}-Q_{i}} \tag{I} \end{gather} \]

The momentum Q is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {Q=mv} \tag{II} \end{gather} \]

substituting expression (II) into expression (I)

\[ \begin{gather} I=mv_{f}-mv_{i} \tag{III} \end{gather} \]

The final velocity can be found using the Principle of Conservation of Mechanical Energy, the initial mechanical energy at the point where the body is released must equal the final mechanical energy at the ground.

\[ \begin{gather} E_{M}^{i}=E_{M}^{f}\\[5pt] U_{i}+K_{i}=U_{f}+K_{f} \end{gather} \]

The Potential Energy is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {U=mgh} \end{gather} \]

the Kinetic Energy is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {K=\frac{mv^{2}}{2}} \end{gather} \]

\[ \begin{gather} \cancel{m}gh_{i}+\frac{\cancel{m}v_{i}^{2}}{2}=\cancel{m}gh_{f}+\frac{\cancel{m}v_{f}^{2}}{2}\\[5pt] gh_{i}+ \frac{v_{i}^{2}}{2}=gh_{f}+\frac{v_{f}^{2}}{2} \tag{IV} \end{gather} \]

For the body of mass m, we have its initial height equal to H (h_i = H), the initial speed is zero (v_i = v_0A = 0), how the body reaches the ground, which is the Reference Level, its final height is zero (h_f = 0), then its final speed (v_f = v_A) will be

\[ \begin{gather} gH+\frac{0^{2}}{2}=g.0+\frac{v_{A}^{2}}{2}\\[5pt] gH=\frac{v_{A}^{2}}{2}\\[5pt] v_{A}^{2}=2gH\\[5pt] v_{A}=\sqrt{2gH\;} \tag{V} \end{gather} \]

substituting expression (V) and the initial speed into expression (III), the impulse of body A, I_A, when reaching the ground will be

\[ \begin{gather} I_{A}=mv_{A}-mv_{0A}\\[5pt] I_{A}=m\sqrt{2gH\;}-m.0\\[5pt] I_{A}=m\sqrt{2gH\;} \tag{VI} \end{gather} \]

For the body of unknown mass M, we have its initial height equal to h (h_i = h), the initial speed is zero (v_i = v_0B = 0), how the body reaches the ground, which is the Reference Level, its final height is zero (h_f = 0), so its final speed (v_f = v_B) will be by the expression (IV)

\[ \begin{gather} gh+\frac{0^{2}}{2}=g.0+\frac{v_{B}^{2}}{2}\\[5pt] gh=\frac{v_{B}^{2}}{2}\\[5pt] v_{B}^{2}=2gh\\[5pt] v_{B}=\sqrt{2gh\;} \tag{VII} \end{gather} \]

substituting expression (VII) and the initial speed into expression (III), the impulse of body B, I_B, when reaching the ground will be

\[ \begin{gather} I_{B}=Mv_{B}-Mv_{0B}\\[5pt] I_{B}=M\sqrt{2gh\;}-M\times 0\\[5pt] I_{B}=M\sqrt{2gh\;} \tag{VIII} \end{gather} \]

Equating expressions (VI) and (VIII)

\[ \begin{gather} I_{A}=I_{B}\\[5pt] m\sqrt{2gH\;}=M\sqrt{2gh\;} \end{gather} \]

Using the property of square roots \( \sqrt{a b\;}=\sqrt{a\;}\sqrt{b\;} \)

we can rewrite the roots of the expression as follows \( \sqrt{2gH\;}=\sqrt{2g\;}\sqrt{H\;} \) and \( \sqrt{2gh\;}=\sqrt{2g\;}.\sqrt{h\;} \)

\[ \begin{gather} m\cancel{\sqrt{2g\;}}\sqrt{H\;}=M\cancel{\sqrt{2g\;}}\sqrt{h\;}\\[5pt] m\sqrt{H\;}=M\sqrt{h\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M=m\frac{\sqrt{H\;}}{\sqrt{h\;}}} \end{gather} \]

Note: Let's assume that m = 1 kg, H = 80 m, and h = 0.2 m, so M is equal to

\[ \begin{gather} M=1\times \sqrt{\frac{80\;}{0.2\;}}\\[5pt] M=\sqrt{400\;}\\[5pt] M=20\;\text{kg} \end{gather} \]

this means that a brick weighing 1 kg falling from a building 80 meters high does the same "damage" as a stone weighing 20 kg falling from a height of 20 centimeters.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .