Solved Problem on Dynamics
advertisement
In the figure, the coefficient of friction between blocks A, B, and the plane on which
they slide is 0.2. The masses of A, B, and C are equal to 100 kg, 50 kg, and 50 kg.
Determine the acceleration of each block and the tension force on the rope. Assume
g = 10 m/s2 and
2aC = aA+aB,
aA, aB and aC are the accelerations of blocks
A, B, and C. The rope and the pulleys are frictionless and lightweight.

Problem data:
- Coefficient of friction between blocks and plane: μ = 0,2;
- Mass of block A: mA = 100 kg;
- Mass of block B: mB = 50 kg;
- Mass of block C: mC = 50 kg;
- Acceleration due to gravity: g = 10 m/s2.
We choose a frame of reference in the same direction as the acceleration, to the right for block A, left to block B, and down to block C (Figure 1-A).
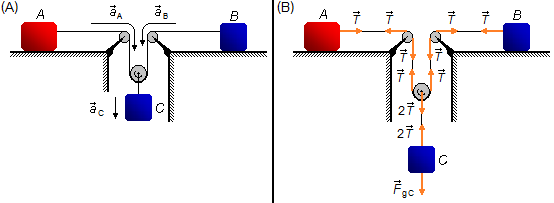
Block A is pulled by the tension force \( \vec{T} \) on the rope, this tension is transferred by the pulley on the left, to the left side of the mobile pulley. On the right side of the mobile pulley, we have the same tension \( \vec{T} \) that is transferred by the fixed pulley from the right to block B. On the rope attached to the mobile pulley, we have a tension force \( 2\vec{T} \) and this tension is balanced by the gravitational force \( {\vec F}_{gC} \) of block C (Figure 1-B).
Solution
Drawing a free-body diagram, we have the forces that act in each of each block and we apply Newton's Second Law
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{I}
\end{gather}
\]
Body A:
- \( {\vec F}_{gA} \): gravitational force on block A;
- \( {\vec N}_{A} \) : normal reaction force of the plane on block A;
- \( {\vec F}_{A f} \): force of friction between the plane and block A;
- \( \vec{T} \): tension force on the rope.
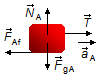
In the vertical direction, there is no motion the gravitational force \( {\vec F}_{gA} \) and the normal reaction force \( {\vec N}_{A} \) balance
\[
\begin{gather}
N_{A}=F_{gA} \tag{II}
\end{gather}
\]
in the horizontal direction, applying the expression (I)
\[
\begin{gather}
T-F_{A f}=m_{A}a_{A} \tag{III}
\end{gather}
\]
Body B:
- \( {\vec F}_{gB} \): gravitational force on block B;
- \( {\vec N}_{B} \): normal reaction force on block B;
- \( {\vec F}_{B f} \): force of friction between the plane and block B;
- \( \vec{T} \): tension force on the rope.
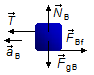
In the vertical direction, there is no motion, the gravitational force \( {\vec F}_{gB} \) and the normal reaction force \( {\vec N}_{B} \) balance
\[
\begin{gather}
N_{B}=F_{gB} \tag{IV}
\end{gather}
\]
in the horizontal direction, applying the expression (I)
\[
\begin{gather}
T-F_{B f}=m_{B}a_{B} \tag{V}
\end{gather}
\]
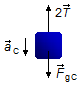
Body C:
- \( {\vec F}_{gC} \): gravitational force on block C;
- \( 2\vec{T} \): tension force on the rope.
\[
\begin{gather}
F_{gC}-2T=m_{C}a_{C} \tag{VI}
\end{gather}
\]
The equations (III), (V), (VI), and the condition given in the problem \( 2a_{C}=a_{A}+a_{B} \), can be written as a system of four equations to four unknowns (aA, aB, aC and T)
\[
\left\{
\begin{array}{l}
T-F_{A f}=m_{A}a_{A}\\
T-F_{B f}=m_{B}a_{B}\\
F_{gC}-2T=m_{C}a_{C}\\
2a_{C}=a_{A}+a_{B}
\end{array}
\right.
\]
solving the first three equations of the system for the accelerations aA,
aB, and aC
\[
\begin{gather}
a_{A}=\frac{T-F_{A f}}{m_{A}} \tag{VII}
\end{gather}
\]
\[
\begin{gather}
a_{B}=\frac{T-F_{B f}}{m_{B}} \tag{VIII}
\end{gather}
\]
\[
\begin{gather}
a_{C}=\frac{F_{gC}-2T}{m_{C}} \tag{IX}
\end{gather}
\]
substituting expressions (VII), (VIII), and (IX) in the fourth equation of the system
\[
\begin{gather}
2\left(\frac{F_{gC}-2T}{m_{C}}\right)=\frac{T-F_{A f}}{m_{A}}+\frac{T-F_{B f}}{m_{B}}\\
\frac{2F_{gC}-4T}{m_{C}}=\frac{T-F_{A f}}{m_{A}}+\frac{T-F_{B f}}{m_{B}} \tag{X}
\end{gather}
\]
The gravitational force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{g}=mg} \tag{XI}
\end{gather}
\]
applying the expression (XI) to bodies A, B and C
\[
\begin{gather}
F_{gA}=m_{A}g \tag{XII-a}
\end{gather}
\]
\[
\begin{gather}
F_{gB}=m_{B}g \tag{XII-b}
\end{gather}
\]
\[
\begin{gather}
F_{gC}=m_{C}g \tag{XII-c}
\end{gather}
\]
The friction force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{f}=\mu N} \tag{XIII}
\end{gather}
\]
applying the expression (XIII) to bodies A and B
\[
F_{A f}=\mu N_{A}
\]
\[
F_{B f}=\mu N_{B}
\]
substituting the normal reaction forces NA and NB
by the expressions (II) and (IV)
\[
F_{A f}=\mu F_{gA}
\]
\[
F_{B f}=\mu F_{gB}
\]
substituting the gravitational forces FgA and FgB
by the expressions (XII-a) and (XII-b)
\[
\begin{gather}
F_{A f}=\mu m_{A}g \tag{XIV-a}
\end{gather}
\]
\[
\begin{gather}
F_{B f}=\mu m_{B}g \tag{XIV-b}
\end{gather}
\]
Substituting expressions (XII-c), (XIV-a), and (XIV-b) into expression (X)
\[
\frac{2m_{C}g-4T}{m_{C}}=\frac{T-\mu m_{A}g}{m_{A}}+\frac{T-\mu m_{B}g}{m_{B}}
\]
substituting numeric values given in the problem
\[
\begin{gather}
\frac{2\times 50\times 10-4T}{50}=\frac{T-0.2\times 100\times 10}{100}+\frac{T-0.2\times 50\times 10}{50}\\
\frac{1000-4T}{50}=\frac{T-200}{100}+\frac{T-100}{50}
\end{gather}
\]
multiplying the numerator and denominator of the term on the left-hand side of the equation, and the second
term on the right side by 2
\[
\begin{gather}
\frac{1000-4T}{50}\times \frac{2}{2}=\frac{T-200}{100}+\frac{T-100}{50}\times \frac{2}{2}\\
\frac{2000-8T}{\cancel{100}}=\frac{T-200}{\cancel{100}}+\frac{2T-200}{\cancel{100}}\\
2000-8T=T-200+2T-200\\
2000+200+200=T+2T+8T\\
11T=2400\\
T=\frac{2400}{11}\\
T=218.2\;\text{N}
\end{gather}
\]
The tension force on the rope attached to bodies A and B will be
T = 218.2 N,
the tension on the rope attached to body C and the mobile pulley will be
2T = 2×218.2 = 436.4 N.
Substituting the gravitational forces given by expressions in (XII) and the friction forces given in (XIV) in the expressions (VII), (VIII), and (IX), the tension force obtained above and the problem data we have the accelerations of the blocks
\[
\begin{gather}
a_{A}=\frac{T-\mu N_{A}}{m_{A}}\\
a_{A}=\frac{T-\mu
m_{A}g}{m_{A}}\\
a_{A}=\frac{218.2-0.2\times 100\times 10}{100}\\
a_{A}=\frac{218.2-200}{100}\\
a_{A}=\frac{18.2}{100}\\
a_{A}=0.182
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{A} \simeq 0.2\;\text{m/s}^{2}}
\]
\[
\begin{gather}
a_{B}=\frac{T-\mu N_{B}}{m_{B}}\\
a_{B}=\frac{T-\mu
m_{B}g}{m_{B}}\\
a_{B}=\frac{218.2-0.2\times 50\times 10}{50}\\
a_{B}=\frac{218.2-100}{50}\\
a_{B}=\frac{118.2}{50}\\
a_{B}=2.364
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{B}\simeq 2.4\;\text{m/s}^{2}}
\]
\[
\begin{gather}
a_{C}=\frac{m_{C}g-2T}{m_{C}}\\
a_{C}=\frac{50\times 10-2\times 218.2}{50}\\
a_{C}=\frac{500-436.4}{50}\\
a_{C}=\frac{63\times 6}{50}\\
a_{C}=1.272
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{C}=1.3\;\text{m/s}^{2}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .