Solved Problem on Coulomb's Law
advertisement
Two equal spheres, charged with electric charges q1 and q2, repel each other with a force of magnitude 2.0×10−3 N when the distance between them is d. Next, the spheres are placed in contact and separated from \( \dfrac{d}{2} \). Under these new conditions, the repulsive force becomes 9.0×10−3 N. Determine the ratio. \( \dfrac{q_{1}}{q_{2}} \).
Problem data:
- Charge of sphere 1: q1;
- Charge of sphere 2: q2;
- Initial distance between spheres: d;
- Initial magnitude of the force between the spheres: Fi = 2.0×10−3 N;
- Final distance between spheres: \( \dfrac{d}{2} \);
- Final magnitude of the force between the spheres: Ff = 9.0×10−3 N;
- Coulomb constant: k.
Problem diagram:
Initially, the spheres are separated by a distance d, and a force Fi acts on them. Then the spheres are placed in contact, and the total charge of the spheres will be distributed equally by the two spheres (Figure 1).
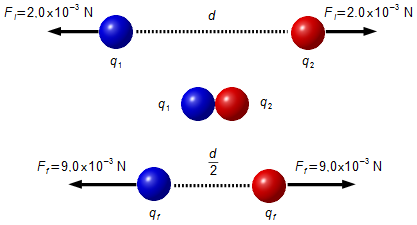
Finally, the spheres are placed at a distance \( \dfrac{d}{2} \), and a force Ff acts on them.
Solution
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{E}=k_{0}\frac{|Q|\;|q|}{r^{2}}} \tag{I}
\end{gather}
\]
Applying expression (I) to the initial situation
\[
\begin{gather}
F_{i}=k\frac{|q_{1}|\;|q_{2}|}{d^{2}}\\[5pt]
2.0\times 10^{-3}=k\frac{q_{1}q_{2}}{d^{2}} \tag{II}
\end{gather}
\]
When the spheres are brought into contact, their charges are distributed equally over the two spheres, and
their final charge will be
\[
\begin{gather}
q_{f}=\frac{q_{1}+q_{2}}{2}
\end{gather}
\]
Applying expression (I) to the final situation
\[
\begin{gather}
F_{f}=k\frac{|q_{f}|\;|q_{f}|}{r^{2}}\\[5pt]
9.0\times 10^{-3}=k\frac{\left(\dfrac{q_{1}+q_{2}}{2}\right)\left(\dfrac{q_{1}+q_{2}}{2}\right)}{\left(\dfrac{d}{2}\right)^{2}}\\[5pt]
9.0\times 10^{-3}=k\frac{\dfrac{\left(q_{1}+q_{2}\right)^{2}}{\cancel{4}}}{\dfrac{d^{2}}{\cancel{4}}}\\[5pt]
9.0\times 10^{-3}=k\frac{\left(q_{1}+q_{2}\right)^{2}}{d^{2}} \tag{III}
\end{gather}
\]
Dividing expression (II) by expression (III)
\[
\begin{gather}
\frac{2.0\times 10^{-3}}{9.0\times 10^{-3}}=\frac{\cancel{k}\dfrac{q_{1}q_{2}}{\cancel{d^{2}}}}{\cancel{k}\dfrac{\left(q_{1}+q_{2}\right)^{2}}{\cancel{d^{2}}}}\\[5pt]
\frac{2.0}{9.0}=\frac{q_{1}q_{2}}{\left(q_{1}+q_{2}\right)^{2}}
\end{gather}
\]
From Special Binomial Products
\( (a+b)^{2}=a^{2}+2ab+b^{2} . \)
\[ (a+b)^{2}=a^{2}+2ab+b^{2} \]
Applying this Special Binomial Product to the denominator on the right-hand side of the equation
\[
\begin{gather}
\frac{2.0}{9.0}=\frac{q_{1}q_{2}}{\left(q_{1}^{2}+2q_{1}q_{2}+q_{2}^{2}\right)}\\[5pt]
2.0\left(q_{1}^{2}+2q_{1}q_{2}+q_{2}^{2}\right)=9.0q_{1}q_{2}\\[5pt]
2.0q_{1}^{2}+4.0q_{1}q_{2}+2.0q_{2}^{2}=9.0q_{1}q_{2}\\[5pt]
2.0q_{1}^{2}+2.0q_{2}^{2}=9.0q_{1}q_{2}-4.0q_{1}q_{2}\\[5pt]
2.0q_{1}^{2}+2.0q_{2}^{2}=5.0q_{1}q_{2}\\[5pt]
2.0\left(q_{1}^{2}+q_{2}^{2}\right)=5.0q_{1}q_{2}\\[5pt]
\frac{q_{1}^{\cancel{2}}}{\cancel{q_{1}}q_{2}}+\frac{q_{2}^{\cancel{2}}}{q_{1}\cancel{q_{2}}}=\frac{5.0}{2.0}\\[5pt]
\frac{q_{1}}{q_{2}}+\frac{q_{2}}{q_{1}}=\frac{5.0}{2.0}\\[5pt]
\frac{q_{1}}{q_{2}}+\frac{q_{2}}{q_{1}}-\frac{5.0}{2.0}=0
\end{gather}
\]
setting the definition
\( x\equiv \dfrac{q_{1}}{q_{2}}\Rightarrow \dfrac{1}{x}\equiv\dfrac{q_{2}}{q_{1}} \)
\[
\begin{gather}
x+\frac{1}{x}-\frac{5.0}{2.0}=0
\end{gather}
\]
multiplying the equation by 2x
\[
\begin{gather}
\qquad\qquad\quad x+\frac{1}{x}-\frac{5}{2}=0\qquad (\times2x)\\[5pt]
2 x\times x+2 \cancel{x}\times \frac{1}{\cancel{x}}-\cancel{2} x\times \frac{5}{\cancel{2}}=0\\[5pt]
2x^{2}+2-5x=0\\[5pt]
2x^{2}-5x+2=0
\end{gather}
\]
Solution of the equation
\( 2x^{2}-5x+2=0 \)
\[
\begin{gather}
\Delta=b^{2}-4ac=(-5)^{2}-4\times 2\times 2=25-16=9\\[10pt]
x=\frac{-b\pm \sqrt{\Delta\;}}{2a}=\frac{-(-5)\pm \sqrt{9\;}}{2\times 2}=\frac{5\pm 3}{4}
\end{gather}
\]
the two roots of the equation are
\[
\begin{gather}
x_{1}=2 \qquad \mathrm{ou} \qquad x_{2}=\frac{1}{2}
\end{gather}
\]
We have two possible solutions
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{q_{1}}{q_{2}}=2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{q_{1}}{q_{2}}=\frac{1}{2}}
\end{gather}
\]
Note: The problem does not provide the values of the charges or which one has the highest
value. The first solution
\( \dfrac{q_{1}}{q_{2}}=2\Rightarrow q_{1}=2q_{2} \)
gives us that the first sphere is charged with a charge that is 2 times greater than the charge on the
second sphere. The second solution
\( \dfrac{q_{1}}{q_{2}}=\frac{1}{2}\Rightarrow q_{2}=2q_{1} \)
gives us that the second sphere is charged with a charge that is 2 times greater than the charge on the
first sphere. The solution to the problem contemplates all the possibilities that correspond to the given
situation.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .