Solved Problem on Circular Motion

A boy turns over his head, a stone tied to a cord with constant speed, and the radius described by the circle made by the stone is 1 m and makes one turn in 2 s. Determine:
a) The speed of the stone;
b) The magnitude of the centripetal acceleration of the stone.

Problem data:

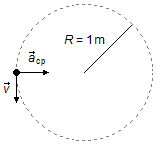
Radius of the trajectory: R = 1 m;
Rotation period: T = 2 s.

Problem diagram:

In the system, we have the velocity \( \vec v \) that is tangent to the trajectory and the centripetal acceleration \( {\vec a}_{cp} \) that acts in the direction of the rope, pointing towards the center of the circle. Centripetal acceleration is responsible for changing the direction of the velocity (it causes the stone to turn).

Figure 1

Solution

a) The speed is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {v=\omega r} \tag{I} \end{gather} \]

where ω is the angular speed given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\omega=\frac{2 \pi}{T}} \tag{II} \end{gather} \]

substituting the equation (II) into equation (I)

\[ \begin{gather} v=\frac{2 \pi}{T} r \end{gather} \]

substituting the problem data and using π = 3.14

\[ \begin{gather} v =\frac{\cancel 2\times 3.14}{\cancel 2\;\mathrm s}\times(1\;\mathrm m) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {v=3.14\;\mathrm{m/s}} \end{gather} \]

b) The magnitude of centripetal acceleration is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {|\;a_{cp}\;|=\frac{v^2}{r}} \end{gather} \]

\[ \begin{gather} |\;a_{cp}\;|=\frac{\left(3.14\;\mathrm{\frac{m}{s}}\right)^2}{1\;\mathrm m}\\[5pt] |\;a_{cp}\;|=\frac{9.86\;\mathrm{\frac{m^{\cancel 2}}{s^2}}}{1\;\mathrm{\cancel m}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {|\;a_{cp}\;|\approx 9.86\;\mathrm{m/s^2}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .