Exercício Resolvido de Calor e Primeira Lei da Termodinâmica
publicidade
Um cilindro contendo n mols de um gás ideal sofre uma transformação adiabática.
a) Partindo da expressão \( W=\int {p\;dV} \) e usando a expressão \( pV^{\gamma }=\text{constante} \), mostre que o trabalho é dado por
\[
W=\left(\frac{1}{\gamma -1}\right)\left(p_{i}V_{i}-p_{f}V_{f}\right)
\]
b) Partindo da Primeira Lei da Termodinâmica na forma diferencial, prove que o trabalho realizado também é
dado por
\[
W=nC_{V}\left(T_{i}-T_{f}\right)
\]
Mostre que este resultado coincide com o que foi obtido no item (a).
Esquema do problema:
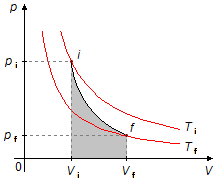
O gás está inicialmente num estado com pressão, volume e temperatura pi, Vi
e Ti, respectivamente, após a transformação adiabática passa para um estado final com
pressão, volume e temperatura pf, Vf e Tf. A área sob a
curva da transformação (em cinza na Figura 1) será igual ao trabalho realizado pelo gás durante a transformação.
a) O trabalho do gás é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{W=\int {p\;dV}} \tag{I}
\end{gather}
\]
Como
\( pV^{\gamma }=\text{constante} \)
para o ponto inicial da transformação temos
\( p_{i}V_{i}^{\gamma }=\text{constante} \),
como esse valor é sempre constante, então para um ponto qualquer da transformação podemos igualar as duas expressões
\[
\begin{gather}
pV^{\gamma }=p_{i}V_{i}^{\gamma}\\
p=p_{i}\frac{V_{i}^{\gamma }}{V^{\gamma }} \tag{II}
\end{gather}
\]
substituindo a expressão (II) na expressão (I)
\[
W=\int {p_{i}\frac{V_{i}^{\gamma }}{V^{\gamma }}\;dV}
\]
sendo pi, e Vi constantes eles podem “sair” da integral, e os limites de
integração vão de Vi a Vf
\[
W=p_{i}V_{i}^{\gamma }\;\int _{V_{i}}^{V_{f}}{\frac{1}{V^{\gamma }}\;dV}
\]
Integral de \( \displaystyle \int _{V_{i}}^{V_{f}}{\dfrac{1}{V^{\gamma }}\;dV} \)
\[
\int _{V_{i}}^{V_{f}}{\frac{1}{V^{\;\gamma }}\;dV=\int_{V_{i}}^{V_{f}}V^{\;-\gamma }\;dV}=\left.\frac{V^{-\gamma +1}}{-\gamma
+1}\;\right|_{\;V_{\;\text{i}}}^{\;V_{\;\text{f}}}=\frac{V_{f}^{\;-\gamma+1}}{-\gamma +1}-\frac
{V_{i}^{-\gamma +1}}{-\gamma+1}=\frac{V_{f}^{1-\gamma }-V_{i}^{1-\gamma }}{1-\gamma }
\]
\[
\begin{gather}
W=p_{i}V_{i}^{\gamma }\frac{V_{f}^{1-\gamma}-V_{i}^{1-\gamma }}{1-\gamma }\\[5pt]
W=\left(\frac{1}{1-\gamma}\right)p_{i}V_{i}^{\gamma }\left(V_{f}^{1-\gamma }-V_{i}^{1-\gamma}\;\right)\\[5pt]
W=\left(\frac{1}{1-\gamma }\right)p_{i}V_{i}^{\gamma}\left(\frac{V_{f}}{V_{f}^{\gamma }}-\frac{V_{i}}{V_{i}^{\gamma}}\right)\\[5pt]
W=\left(\frac{1}{1-\gamma }\right)\left(p_{i}V_{i}^{\gamma}\frac{V_{f}}{V_{f}^{\gamma }}-p_{i}V_{i}^{\gamma}\frac{V_{i}}{V_{i}^{\gamma }}\right)\\[5pt]
W=\left(\frac{1}{1-\gamma}\right)\left(\frac{p_{i}V_{i}^{\gamma }V_{f}}{V_{f}^{\gamma}}-p_{i}V_{i}\right) \tag{III}
\end{gather}
\]
Usando novamente a condição
\( pV^{\gamma }=\text{constante} \)
entre os pontos inicial e final da transformação
\[
\begin{gather}
p_{i}V_{i}^{\gamma }=p_{f}V_{f}^{\gamma}\\
p_{f}=\frac{p_{i}V_{i}^{\gamma }}{V_{f}^{\gamma }} \tag{IV}
\end{gather}
\]
substituindo a expressão (IV) na expressão (III)
\[
\begin{gather}
W=\left(\frac{1}{1-\gamma}\right)\left(p_{f}V_{f}-p_{i}V_{i}\right)\\[5pt]
W=\left(\frac{1}{-(-1+\gamma)}\right)\left(p_{f}V_{f}-p_{i}V_{i}\right)\\[5pt]
W=-\left(\frac{1}{\gamma-1}\right)\left(p_{f}V_{f}-p_{i}V_{i}\right)
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{W=\left(\frac{1}{\gamma -1}\right)\left(p_{i}V_{i}-p_{f}V_{f}\right)}
\]
b) Como a transformação é adiabática o calor trocado com o meio é nulo (Q = 0) e a Primeira Lei da Termodinâmica se reduz a U = −W, que na forma diferencial é escrita como
\[
dU=nC_{V}\;dT=-p\;dV
\]
onde CV é a Capacidade Térmica a Volume Constante e como
\( dW=p\;dV \)
podemos reescrever
\[
\begin{gather}
-dW=nC_{V}\;dT\\
dW=-nC_{V}\;dT
\end{gather}
\]
integrando de ambos os lados da igualdade
\[
\int dW=\int -nC_{V}\;dT
\]
do lado esquerdo da igualdade os limites de integração vão de zero até W, do lado direito da igualdade o fator
\( -nC_{V} \)
é constante e pode “sair” da integral, os limites de integração vão de Ti a Tf
\[
\int _{0}^{W}dW=-nC_{V}\int _{T_{i}}^{T_{f}}dT
\]
Integral de \( \displaystyle \int_{0}^{W}{{dW}} \)
\[
\int _{0}^{W}{{dW}}=\left.W\right|_{\;0}^{\;W}=W-0=W
\]
Integral de \( \displaystyle \int_{T_{\;i}}^{\;T_{f}}{{dT}} \)
\[
\int_{T_{i}}^{T_{f}}{{dT}}=\left.T\;\right|_{\;T_{i}}^{\;T_{f}}=T_{f}-T_{i}
\]
\[
W=-nC_{V}\left(T_{f}-T_{i}\right)
\]
\[ \bbox[#FFCCCC,10px]
{W=nC_{V}\left(T_{i}-T_{f}\right)}
\]
Usando a Equação de Estado dos Gases Ideais ou Equação de Clapeyron
\[ \bbox[#99CCFF,10px]
{pV=nRT}
\]
escrevemos esta equação para os estados inicial e final da transformação
\[
\begin{gather}
p_{i}V_{i}=nRT_{i}\Rightarrow T_{i}=\frac{p_{i}V_{i}}{nR} \tag{V-a}\\[10px]
p_{f}V_{f}=nRT_{f}\Rightarrow T_{f}=\frac{p_{f}V_{f}}{nR} \tag{V-b}
\end{gather}
\]
onde R é a Constante Universal dos Gases Perfeitos, substituindo as expressões (V-a) e (V-b) no
resultado acima
\[
\begin{gather}
W=nC_{V}\left(\frac{p_{i}V_{i}}{nR}-\frac{p_{f}V_{f}}{nR}\right)\\[5pt]
W=\frac{nC_{V}}{nR}\left(p_{i}V_{i}-p_{f}V_{f}\right)\\[5pt]
W=\frac{C_{V}}{R}\left(p_{i}V_{i}-p_{f}V_{f}\right) \tag{VI}
\end{gather}
\]
Das seguintes expressões
\[
\begin{gather}
\bbox[#99CCFF,10px]
{C_{p}-C_{V}=R} \tag{VII-a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\gamma =\frac{C_{p}}{C_{V}}} \tag{VII-b}
\end{gather}
\]
onde Cp é a Capacidade Térmica a Pressão Constante, da expressão (VII-b)
\[
C_{p}=\gamma C_{V}
\]
substituindo na expressão (VII-a)
\[
\begin{gather}
\gamma C_{V}-C_{V}=R\\[5pt]
C_{V}(\gamma-1)=R\\[5pt]
\frac{C_{V}}{R}=\frac{1}{\gamma -1} \tag{VIII}
\end{gather}
\]
substituindo a expressão (VIII) na expressão (VI)
\[ \bbox[#FFCCCC,10px]
{W=\left(\frac{1}{\gamma -1}\right)\left(p_{i}V_{i}-p_{f}V_{f}\right)} \tag{Q.E.D.}
\]
Observação: Q.E.D. é a abreviação da expressão em latim “quod erat demosntrandum” que
significa “como queríamos demonstrar”.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .