Exercício Resolvido de Cinemática
publicidade
Obtenha a velocidade e a aceleração de um corpo se movendo num plano em coordenadas polares.
Esquema do problema:
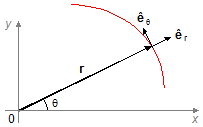
Em coordenadas polares um ponto em uma trajetória é descrito por um vetor posição r formando um
ângulo θ com o eixo-x. No ponto considerado a direção do vetor posição e da variação do
ângulo sãp dados pelos vetores unitários êr e êθ.
Solução
O vetor posição em coordenadas polares é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{r}=r\;{\mathbf{ê}}_{r}} \tag{I}
\end{gather}
\]
O vetor velocidade do corpo é dado pela derivada em relação ao tempo
\[ \bbox[#99CCFF,10px]
{\mathbf{v}=\frac{d\mathbf{r}}{dt}}
\]
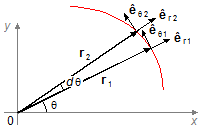
Quando o corpo se desloca sobre a trajetória ao longo do tempo os vetores unitários em coordenadas
polares também mudam de posição. Isto quer dizer que estes vetores não são constantes no espaço (a sua
direção muda ponto a ponto na trajetória – Figura 2).
Derivada de \( r\;{\mathbf{ê}}_{r} \)
Derivando o produto de funções na forma
Derivando o produto de funções na forma
\[
(uv)' = u' v+u v'
\]
onde
\( u=r \)
e
\( v={\mathbf{ê}}_{r} \),
\( u'=\dfrac{dr}{dt} \)
e
\( v'=\dfrac{d{\mathbf{ê}}_{r}}{dt} \)
\[
\frac{d(r\;{\mathbf{ê}}_{r})}{dt} = \frac{dr}{dt}\;{\mathbf{ê}}_{r}+r\;\frac{d{\mathbf{ê}}_{r}}{dt}
\]
\[
\mathbf{v}=\frac{d\mathbf{r}}{dt}=\frac{dr}{dt}\;{\mathbf{ê}}_{r}+r\;\frac{d{\mathbf{ê}}_{r}}{dt}
\]
Interpretação dos termos \( \dfrac{d{\mathbf{ê}}_{r}}{dt} \) e
\( \dfrac{d{\mathbf{ê}}_{\theta}}{dt} \)
1.º método
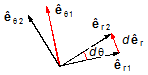
Figura 3: Na figura o vetor deslocamento dêr não parece
perfeitamente paralelo ao vetor unitário êθ, isto porque
dθ está exagerado, se o ângulo é infinitamente pequeno os vetores
êr1 e êr2 ficam próximos e
dêr fica paralelo a êθ.
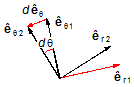
Figura 4: Na figura o vetor deslocamento dêθ não parece
perfeitamente paralelo ao vetor unitário êr, isto porque
dθ está exagerado, se o ângulo é infinitamente pequeno os vetores
êθ1 e êθ2 ficam próximos e
dêθ fica paralelo a êr e apontando no
sentido contrário.
2.º método
A posição dos vetores unitários êr e êθ mudam com o valor do ângulo θ e o ângulo varia com o tempo, portanto êr e êθ são funções compostas do tipo
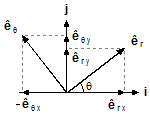
Figura 5
Derivando a expressão (V) em relação a θ
Derivando a expressão (VI) em relação a θ
3.º método
Calculando o produto escalar
Calculando o produto escalar
1.º método
Quando o corpo sofre um deslocamento infinitesimal dθ, o vetor unitário na direção radial
se desloca de êr1 para êr2 e o vetor deslocamento
infinitesimal será (Figura 3)
\[
d{\mathbf{ê}}_{r}={\mathbf{ê}}_{r2}-{\mathbf{ê}}_{r1}
\]
este vetor será perpendicular ao vetor unitário êr, e portanto, estará na mesma
direção e sentido que o vetor unitário êθ
\[
d{\mathbf{ê}}_{r}=d\theta\;{\mathbf{ê}}_{\theta}
\]
dividindo ambos os membros da igualdade por dt
\[
\begin{gather}
\frac{d{\mathbf{ê}}_{r}}{dt}=\frac{d\theta}{dt}{\mathbf{ê}}_{\theta} \tag{II}
\end{gather}
\]

Quando o corpo sofre um deslocamento infinitesimal dθ o vetor unitário na direção angular se
desloca de êθ1 para êθ2 e o vetor deslocamento infinitesimal
será (Figura 4)
\[
d{\mathbf{ê}}_{\theta}={\mathbf{ê}}_{\theta 2}-{\mathbf{ê}}_{\theta1}
\]
este vetor será perpendicular ao vetor unitário êθ, e portanto, estará na mesma
direção e sentido contrário ao vetor unitário êr
\[
d{\mathbf{ê}}_{\theta}=-d\theta\;{\mathbf{ê}}_{r}
\]
dividindo ambos os membros da igualdade por dt
\[
\begin{gather}
\frac{d{\mathbf{ê}}_{\theta}}{dt}=-\frac{{d\theta}}{dt}\;{\mathbf{ê}}_{r} \tag{III}
\end{gather}
\]

2.º método
A posição dos vetores unitários êr e êθ mudam com o valor do ângulo θ e o ângulo varia com o tempo, portanto êr e êθ são funções compostas do tipo
\[
{\mathbf{e}}_{r}[\theta(t)] \qquad \text{e} \qquad {\mathbf{e}}_{\theta}[\theta(t)]
\]
As derivadas são dadas pela regra da cadeia
\[
\begin{gather}
\frac{d{\mathbf{e}}_{r}[\theta(t)]}{dt}=\frac{d{\mathbf{e}}_{r}}{d\theta}\frac{d\theta}{dt}
\qquad \text{e} \qquad
\frac{d{\mathbf{e}}_{\theta}[\theta(t)]}{dt}=\frac{d{\mathbf{e}}_{r}}{d\theta}\frac{d\theta}{dt} \tag{IV}
\end{gather}
\]
Se decompusermos os vetores unitários êr e êθ do
sistema de coordenadas polares nas direções i e j do sistema de coordenadas
cartesianas, podemos escrever (Figura 5)
\[
\begin{gather}
{\mathbf{ê}}_{r}={\mathbf{ê}}_{rx}+{\mathbf{ê}}_{ry}\\
{\mathbf{ê}}_{\theta}={\mathbf{ê}}_{\theta x}+{\mathbf{ê}}_{\theta y}
\end{gather}
\]
\[
\begin{gather}
{\mathbf{ê}}_{r}=\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j} \tag{V}\\
{\mathbf{ê}}_{\theta}=-\operatorname{sen}\theta\;\mathbf{i}+\cos \theta\;\mathbf{j} \tag{VI}
\end{gather}
\]

Derivando a expressão (V) em relação a θ
\[
\frac{d{\mathbf{ê}}_{r}}{d\theta}=-\operatorname{sen}\theta\;\mathbf{i}+\cos \theta\;\mathbf{j}={\mathbf{ê}}_{\theta}
\]
substituindo este valor na primeira das expressões (IV)
\[
\frac{d{\mathbf{ê}}_{r}}{dt}=\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}
\]
que coincide com a expressão (II) acima.Derivando a expressão (VI) em relação a θ
\[
\frac{d{\mathbf{ê}}_{\theta}}{d\theta}=-\cos \theta\;\mathbf{i}+(-\operatorname{sen}\theta\;\mathbf{j})=-\cos \theta\;\mathbf{i}-\operatorname{sen}\theta\;\mathbf{j}=-(\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j})=-{\mathbf{ê}}_{r}
\]
substituindo este valor na segunda das expressões (IV)
\[
\frac{d{\mathbf{ê}}_{\theta}}{dt}=-{\frac{d\theta}{dt}}\;{\mathbf{ê}}_{r}
\]
que coincide com a expressão (III) acima.
3.º método
Calculando o produto escalar
\[
{\mathbf{ê}}_{r}.{\mathbf{ê}}_{r}=\left|\;{\mathbf{ê}}_{r}\;\right|.\left|\;{\mathbf{ê}}_{r}\;\right|.\operatorname{sen}0=1
\]
derivando esta expressão em relação a θ
\[
\begin{gather}
\frac{d{\mathbf{ê}}_{r}}{d\theta}.{\mathbf{ê}}_{r}+{\mathbf{ê}}_{r}.\frac{d{\mathbf{ê}}_{r}}{d\theta}=\frac{d(1)}{d\theta}\\
2\;{\mathbf{ê}}_{r}.\frac{d{\mathbf{ê}}_{r}}{d\theta}=0\\
{\mathbf{ê}}_{r}.\frac{d{\mathbf{ê}}_{r}}{d\theta}=0
\end{gather}
\]
para que este produto escalar seja nulo o vetor
\( \left(\frac{d{\mathbf{ê}}_{r}}{d\theta}\right) \)
deve ser perpendicular ao vetor êr, lembrando que
\( \operatorname{sen}\frac{\pi}{2}=0 \),
portanto ele está na mesma direção que o vetor êθ, e pela Figura 3 seu sentido é
positivo
\[
\frac{d{\mathbf{ê}}_{r}}{d\theta}={\mathbf{ê}}_{\theta}
\]
substituindo este valor na primeira das expressões (IV)
\[
\frac{d{\mathbf{ê}}_{r}}{dt}=\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}
\]
que coincide com a expressão (II) acima.
Calculando o produto escalar
\[
{\mathbf{ê}}_{\theta}.{\mathbf{ê}}_{\theta}=\left|\;{\mathbf{ê}}_{\theta}\;\right|.\left|\;{\mathbf{ê}}_{\;\theta}\;\right|.\operatorname{sen}0=1
\]
derivando esta expressão em relação a θ
\[
\begin{gather}
\frac{d{\mathbf{ê}}_{\theta}}{d\theta}.{\mathbf{ê}}_{\theta}+{\mathbf{ê}}_{\theta}.\frac{d{\mathbf{ê}}_{\theta}}{d\theta}=\frac{d(1)}{d\theta}\\
2\;{\mathbf{ê}}_{\theta}.\frac{d{\mathbf{ê}}_{\theta}}{d\theta}=0\\
{\mathbf{ê}}_{\theta}.\frac{d{\mathbf{ê}}_{\theta}}{d\theta}=0
\end{gather}
\]
para que este produto escalar seja nulo o vetor
\( \left(\frac{d{\mathbf{ê}}_{\theta}}{d\theta}\right) \)
deve ser perpendicular ao vetor êθ, lembrando que
\( \operatorname{sen}\frac{\pi}{2}=0 \),
portanto ele está na mesma direção que o vetor êr, e pela Figura 4 seu sentido é
negativo
\[
\frac{d{\mathbf{ê}}_{\theta}}{d\theta}=-{\mathbf{ê}}_{r}
\]
substituindo este valor na segunda das expressões (IV)
\[
\frac{d{\mathbf{ê}}_{\theta}}{dt}=-{\frac{d\theta}{dt}}\;{\mathbf{ê}}_{r}
\]
que coincide com a expressão (III) acima.
usando a interpretação feita em (II)
\[ \bbox[#FFCCCC,10px]
{\mathbf{v}=\frac{dr}{dt}\;\mathbf{ê}_{r}+r\frac{d\theta}{dt}{\mathbf{ê}}_{\theta}}
\]
O vetor aceleração é dado pela derivada em relação ao tempo da expressão acima
\[
\mathbf{a}=\frac{d\mathbf{v}}{dt}=\frac{d}{dt}\left(\frac{dr}{dt}\;{\mathbf{ê}}_{r}+r\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}\right)
\]
Derivada de \( \dfrac{dr}{dt}\;\mathbf{ê}_{r} \)
pela regra do produto:
pela regra do produto:
\[
\frac{d}{dt}\left(\frac{dr}{dt}\;{\mathbf{ê}}_{r}\right)=\frac{d}{dt}\left(\frac{dr}{dt}\right)\;{\mathbf{ê}}_{r}+\frac{dr}{dt}\frac{d\mathbf{ê}_{r}}{dt}
\]
usando a interpretação feita em (II)
\[
\frac{d}{dt}\left(\frac{dr}{dt}\;{\mathbf{ê}}_{r}\right)=\frac{d^{2}r}{dt^{2}}\;{\mathbf{ê}}_{r}+\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{ê}}_{\;\theta}
\]
Derivada de \( r\dfrac{d\theta}{dt}\;{\mathbf{ê}}_{\theta} \)
derivando o produto de funções na forma:
derivando o produto de funções na forma:
\[
(uvw)' = u' v w+uv'w+u v w'
\]
\[
\frac{d}{dt}\left(r\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}\right)=\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}+r\frac{d}{dt}\left(\frac{d\theta}{dt}\right)\;{\mathbf{ê}}_{\theta}+r\frac{d\theta}{dt}\frac{d{\mathbf{ê}}_{\theta}}{dt}
\]
usando a interpretação feita em (III)
\[
\begin{gather}
\frac{d}{dt}\left(r\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}\right)=\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{ê}}_{\theta}-r\frac{d\theta}{dt}\frac{d\theta}{dt}\;{\mathbf{ê}}_{r}\\
\frac{d}{dt}\left(r\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}\right)=\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{ê}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{ê}}_{\theta}-r\left(\frac{d\theta}{dt}\right)^{2}{\mathbf{ê}}_{r}
\end{gather}
\]
Observação: Não confundir
\( \frac{d}{dt}\left(\frac{d\theta}{dt}\right)=\frac{d^{2}\theta}{dt^{2}} \)
com
\( \frac{d\theta}{dt}\frac{d\theta}{dt}=\left(\frac{d\theta}{dt}\right)^{2} \),
no primeiro caso a derivada segunda do espaço angular em relação ao tempo representa a aceleração
angular (γ), no segundo caso a derivada primeira do espaço angular em relação ao tempo representa a
velocidade angular (ω) elevada ao quadrado, é a velocidade angular ao quadrado (ω2).
\[
\begin{gather}
\mathbf{a}=\frac{d^{2}r}{dt^{2}}\;{\mathbf{ê}}_{r}+\frac{dr}{dt}\;\frac{d\theta}{dt}{\mathbf{ê}}_{\theta}+\frac{dr}{dt}\frac{d\theta}{dt}{\mathbf{ê}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}{\mathbf{ê}}_{\theta}-r\left(\frac{d\theta}{dt}\right)^{2}{\mathbf{ê}}_{r}\\
\mathbf{a}=\frac{d^{2}r}{dt^{2}}\;{\mathbf{ê}}_{r}+2\frac{dr}{dt}\;\frac{d\theta}{dt}{\mathbf{ê}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{ê}}_{\theta}-r\left(\frac{d\theta}{dt}\right)^{2}{\mathbf{ê}}_{r}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{a}=\left[\frac{d^{2}r}{dt^{2}}-r\left(\frac{d\theta}{dt}\right)^{2}\right]\;{\mathbf{ê}}_{r}+\left[2\frac{dr}{dt}\frac{d\theta}{dt}+r\frac{d^{2}\theta}{dt^{2}}\right]\;{\mathbf{ê}}_{\theta}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .