Exercício Resolvido de Dilatação
publicidade
Um tubo capilar de um termômetro de mercúrio graduado de 0 a 100° C tem diâmetro 1/10 mm, seu reservatório é cilíndrico com 1 cm de comprimento e 2 mm de raio. Determinar o comprimento correspondente a cada grau da haste. Sendo os coeficientes de dilatação do mercúrio e do vidro respectivamente: \( \gamma_{Hg}=\dfrac{1}{5550}\;°\text{C}^{-1} \) e \( \gamma_{V}=\dfrac{1}{38850}\;°\text{C}^{-1} \)
Dados do problema:
- Diâmetro do tubo: \( d_{T}=\dfrac{1}{10}\;\text{mm} \);
- Comprimento do reservatório: HR = 1 cm;
- Raio do reservatório: RR = 2 mm;
- Variação da temperatura: Δt = 1 °C;
- Coeficiente de dilatação volumétrica do mercúrio: \( \gamma_{Hg}=\dfrac{1}{5550}\;°\text{C}^{-1} \);
- Coeficiente de dilatação volumétrica do vidro: \( \gamma_{V}=\dfrac{1}{38850}\;°\text{C}^{-1} \).
Inicialmente o termômetro está numa temperatura t, quando o sistema é aquecido de 1 °C ele passa a uma temperatura t+1 (Δt = 1 °C) ele se expande em todas as direções, como o mercúrio possui um coeficiente de dilatação maior que o do vidro ele se expande mais que o reservatório onde está e sobe um pouco mais pelo capilar (Figura 1)
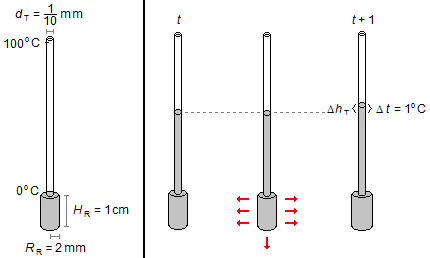
Quando a temperatura sofre esta variação Δt a altura da coluna de mercúrio sofre uma variação ΔhT.
Solução
Em primeiro lugar devemos converter o diâmetro do tubo e o raio do reservatório, dados em milímetros (mm), e o comprimento do reservatório, dado em centímetros (cm), para metros (m) usado no Sistema Internacional (S.I.)
\[
\begin{gather}
d_{T}=\frac{1}{10}\;\text{mm}=0,1\text{mm}=0,1.10^{-3}\;\text{m}=1.10^{-1}.10^{-3}\;\text{m}=1.10^{-4}\;\text{m}\\[5pt]
R_{R}=2\;\text{mm}=2.10^{-3}\;\text{m}\\[5pt]
H_{R}=1\;\text{cm}=1.10^{-2}\;\text{m}
\end{gather}
\]
A variação do volume do mercúrio no tubo (ΔVT, volume aparente) será a diferença
entre a variação total do volume do mercúrio (ΔVHg) e a variação do volume do
reservatório ΔVR
\[
\begin{gather}
\Delta V_{T}=\pi \left(\frac{d_{T}}{2}\right)^{2}\Delta h_{T} \tag{I}
\end{gather}
\]
A dilatação volumétrica é dada por
\[ \bbox[#99CCFF,10px]
{V=V_{0}(1+\gamma \Delta t)}
\]
a variação total do volume é dada por
\[
\begin{gather}
V=V_{0}+V_{0}\gamma \Delta t\\
V-V_{0}=V_{0}\gamma \Delta t\\
\Delta V=V_{0}\gamma \Delta t \tag{II}
\end{gather}
\]
Aplicando a expressão (II), variação total do volume do mercúrio é dada por
\[
\begin{gather}
\Delta V_{Hg}=V_{0Hg}\gamma_{Hg}\Delta t \tag{III}
\end{gather}
\]
e a variação total do volume do reservatório é dada por
\[
\begin{gather}
\Delta V_{R}=V_{0R}\gamma_{V}\Delta t \tag{IV}
\end{gather}
\]
Substituindo as expressões (III) e (IV) na expressão (I)
\[
\Delta V_{T}=V_{0Hg}\gamma_{Hg}\Delta t-V_{0R}\gamma_{V}\Delta t
\]
como inicialmente o mercúrio ocupa todo o volume do reservatório
V0Hg = V0R
(e uma certa altura do tubo capilar), colocando V0RΔt em evidência
\[
\begin{gather}
\Delta V_{T}=V_{0R}\gamma_{Hg}\Delta t-V_{0R}\gamma_{V}\Delta t\\
\Delta V_{T}=V_{0R}\Delta t(\gamma_{Hg}-\gamma_{V}) \tag{V}
\end{gather}
\]
O volume de um cilindro é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V=\pi r^{2}h} \tag{VI}
\end{gather}
\]
a variação do volume do tubo será
\[
\begin{gather}
\Delta V_{T}=\pi \left(\frac{d_{T}}{2}\right)^{2}\Delta h_{T} \tag{VII}
\end{gather}
\]
o raio do tubo será metade do diâmetro dado no problema
\[ \bbox[#99CCFF,10px]
{r=\frac{d}{2}}
\]
\[
\begin{gather}
r_{T}=\frac{d_{T}}{2} \tag{VIII}
\end{gather}
\]
substituindo a expressão (VIII) na expressão (VII)
\[
\begin{gather}
\Delta V_{T}=\pi \left(\frac{d_{T}}{2}\right)^{2}\Delta h_{T} \tag{IX}
\end{gather}
\]
O reservatório tem formato cilíndrico, usando a expressão (VI) seu volume será
\[
\begin{gather}
V_{0R}=\pi R_{R}^{2}H_{R} \tag{X}
\end{gather}
\]
Substituindo as expressões (VII) e (X) na expressão (V)
\[
\begin{gather}
\cancel{\pi} \left(\frac{d_{T}}{2}\right)^{2}\Delta h_{T}=\cancel{\pi} R_{R}^{2}H_{R}\Delta t(\gamma_{Hg}-\gamma_{V})\\[5pt]
\Delta h_{T}=\frac{R_{R}^{2}H_{R}\Delta t(\gamma_{Hg}-\gamma_{V})}{\left(\dfrac{d_{T}}{2}\right)^{2}}\\[5pt]
\Delta h_{T}=\frac{R_{R}^{2}H_{R}\Delta t(\gamma_{Hg}-\gamma_{V})}{\dfrac{d_{T}^{2}}{4}}\\[5pt]
\Delta h_{T}=\frac{4R_{R}^{2}H_{R}\Delta t(\gamma_{Hg}-\gamma_{V})}{d_{T}^{2}}
\end{gather}
\]
substituindo os dados do problema
\[
\begin{gather}
\Delta h_{T}=\frac{4.(2.10^{-3})^{2}.1.10^{-2}.1.\left(\dfrac{1}{5550}-\dfrac{1}{38850}\right)}{(1.10^{-4})^{2}}\\[5pt]
\Delta h_{T}=\frac{4.4.10^{-6}.1.10^{-2}.1.\left(18.10^{-5}-2,6.10^{-5}\right)}{1.10^{-8}}\\[5pt]
\Delta h_{T}=16.10^{-8}.\left(15,4.10^{-5}\right).10^{8}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\Delta h_{T}=2,5.10^{-3}\;\text{m}^{3}=2,5\;\text{mm}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .