Exercício Resolvido de Lentes
publicidade
Uma lente delgada biconvexa cujos raios de curvatura são iguais a 42 cm, tem índice de refração 1,7. Introduz-se essa lente num cuba transparente de faces paralelas, verticais e de espessura desprezível. A espessura da cuba é ligeiramente superior à da lente.
a) Estando a cuba vazia, calcular a que distância do conjunto deve ser colocado um anteparo para que receba a imagem de um objeto situado a 90 cm daquele conjunto;
b) Enche-se a cuba com um líquido de índice n'. Calcular a distância focal (F), do sistema formado, em função de n' e construir a curva F = f(n') dando a n' os valores de 1 a 1,9 com incremento de 0,1.
c) Supondo mantida fixa a posição do objeto, calcular a que distância do sistema deve ser colocado o anteparo para receba a sua imagem, supõe-se neste caso n'=1,2.
Dados do problema:
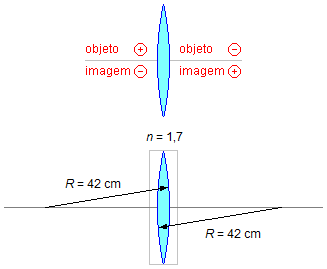
- Raio de curvatura (usando a convenção de que para a superfície convexa o raio é positivo), lente biconvexa.
- Superfície convexa: R = 42 cm;
- Índice de refração: n2 = 1,7;
- Adotando que a lente está inicialmente no ar, índice de refração do ar: n1 = 1.
Adotando-se a convenção de sinais onde do lado da luz incidente temos a abscissa positiva para o objeto real (p > 0) e negativa para a imagem virtual (p' < 0), do lado oposto temos a abscissa do objeto virtual negativa (p < 0) e positiva para a imagem real (p' > 0), Figura 1.
a) A distância focal é dada pela Fórmula dos Fabricantes de Lentes ou Equação de Halley
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{1}{f}=\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)} \tag{I}
\end{gather}
\]
como a lente é biconvexa, temos seus raios de curvaturas iguais
(R1 = R2 = R = 42 cm – Figura 1), substituindo os dados temos o
valor de
\( \dfrac{1}{f} \)
\[
\begin{gather}
\frac{1}{f}=\left(\frac{1,7}{1}-1\right)\left(\frac{1}{42}+\frac{1}{42}\right)\\
\frac{1}{f}=\left(1,7-1\right)\left(\frac{2}{42}\right)\\
\frac{1}{f}=0,7.\frac{1}{21}
\end{gather}
\]
dividindo o numerador e o denominador por 0,7
\[
\begin{gather}
\frac{1}{f}=\frac{0,7:0,7}{21:0,7}\\
\frac{1}{f}=\frac{1}{30} \tag{II}
\end{gather}
\]
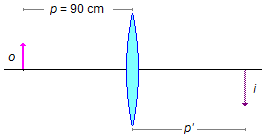
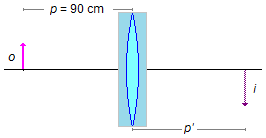
Como a cuba é muito fina e está vazia podemos desprezá-la e o problema se reduz ao cálculo da posição
da imagem (p') de um objeto colocado a uma distância p (Figura 2), usando a
Equação dos Pontos Conjugados
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{1}{f}=\frac{1}{p}+\frac{1}{p'}} \tag{III}
\end{gather}
\]
substituindo a expressão (II) na expressão (III) e a distância dada no problema
\[
\begin{gather}
\frac{1}{30}=\frac{1}{90}+\frac{1}{p'}\\
\frac{1}{p'}=\frac{1}{30}-\frac{1}{90}
\end{gather}
\]
o Mínimo Múltiplo Comum (M.M.C.) entre 30 e 90 é 90
\[
\begin{gather}
\frac{1}{p'}=\frac{3-1}{90}\\
\frac{1}{p'}=\frac{2}{90}\\
p'=\frac{90}{2}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{p'=45\;\text{cm}}
\]
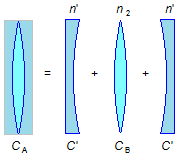
b) Com a cuba cheia de líquido o sistema passa a se comportar como uma associação de lentes, a lente
original biconvexa entre duas lentes plano-côncavas com índice de refração igual ao do líquido
(n'), Figura 3.
Para uma associação de lentes a convergência do sistema (CA) será a soma da convergência de cada lente, a convergência é dada por
Para uma associação de lentes a convergência do sistema (CA) será a soma da convergência de cada lente, a convergência é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{C=\frac{1}{f}} \tag{IV}
\end{gather}
\]
igualando as expressões (I) e (IV) a convergência pode ser calculada por
\[
\begin{gather}
C=\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right) \tag{V}
\end{gather}
\]
A convergência da lente biconvexa foi calculada no item (a) pela expressão (II)
\[
C_{B}=\frac{1}{f}=\frac{1}{30}
\]
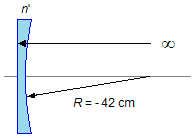
Para lentes côncavas o raio é negativo, as duas lentes formadas pelo líquido terão o mesmo raio que a
lente biconvexa com sinal negativo (−42 cm), para a face plana o raio está no infinito (∞),
Figura 4. Aplicando a expressão (V), a convergência (C') dessas lentes será
\[
C'=\left(\frac{n'}{1}-1\right)\left(\frac{1}{\infty}+\frac{1}{-42}\right)
\]
a fração
\( \frac{1}{\infty} \)
será igual a zero, quanto maior o denominador menor será o resultado da divisão
\[
\begin{gather}
C'=\left(n'-1\right)\left(0-\frac{1}{42}\right)\\
C'=-{\frac{n'-1}{42}}
\end{gather}
\]
A convergência da associação será
\[
\begin{gather}
C_{A}=C'+C_{B}+C'\\
C_{A}=2C'+C_{B}
\end{gather}
\]
substituindo os valores de C' e CB
\[
\begin{gather}
C_{A}=-2\frac{n'-1}{42}+\frac{1}{30}\\
C_{A}=-{\frac{n'-1}{21}}+\frac{1}{30}
\end{gather}
\]
o Mínimo Múltiplo Comum (M.M.C.) entre 21 e 30 é 210
\[
\begin{gather}
C_{A}=\frac{-10(n'-1)+7}{210}\\
C_{A}=\frac{-10n'+10+7}{210}\\
C_{A}=\frac{17-10n'}{210}
\end{gather}
\]
invertendo a expressão (I) encontramos a distância focal F da associação
\[
\begin{gather}
F=\frac{1}{C_{A}}\\
F=\frac{1}{\dfrac{17-10n'}{210}}
\end{gather}
\]
a distância focal do sistema em função de n' será
\[ \bbox[#FFCCCC,10px]
{F(n')=\frac{210}{17-10n'}}
\]
Para fazer o gráfico desta função fazemos a tabela seguinte
| n' | \( F(n')=\frac{210}{17-10n'} \) | F(n') |
|---|---|---|
| 1,0 | \( F(n')=\frac{210}{17-10.1,0} \) | 30 |
| 1,1 | \( F(n')=\frac{210}{17-10.1,1} \) | 35 |
| 1,2 | \( F(n')=\frac{210}{17-10.1,2} \) | 42 |
| 1,3 | \( F(n')=\frac{210}{17-10.1,3} \) | 52,5 |
| 1,4 | \( F(n')=\frac{210}{17-10.1,4} \) | 69,9 |
| 1,5 | \( F(n')=\frac{210}{17-10.1,5} \) | 105 |
| 1,6 | \( F(n')=\frac{210}{17-10.1,6} \) | 210 |
| 1,7 | \( F(n')=\frac{210}{17-10.1,7} \) | indefinido |
| 1,8 | \( F(n')=\frac{210}{17-10.1,8} \) | −210 |
| 1,9 | \( F(n')=\frac{210}{17-10.1,9} \) | −105 |
Tabela 1
Para n' = 1,7 o denominador é zero, como não se pode dividir por zero o resultado da função é indefinido. Colocando esses valores num gráfico
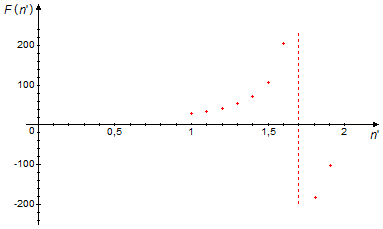
Observação: A lente biconvexa usada é uma lente de bordo delgado e índice de refração 1,7.
Para os valores de n' entre 1 e 1,6, o índice de refração da lente é maior que o índice de refração
do meio (líquido) e a lente tem comportamento convergente, foco positivo (F > 0) Para os valores
de n' entre 1,8 e 1,9, o índice de refração da lente é menor que o índice de refração do meio e a
lente tem comportamento divergente, foco negativo (F < 0). Para n' igual a 1,7 a lente tem
o mesmo índice de refração que o meio, o sistema se comporta como se a lente não existisse e a luz passa
direto sem sofrer desvio.
c) A distância focal do sistema é dada pela expressão encontrada no item (b), procurando na tabela construída o valor de n' = 1,2 encontramos para a distância focal F = 42 cm (Figura 5).
Usando a expressão (III)
\[
\begin{gather}
\frac{1}{F}=\frac{1}{p}+\frac{1}{p'}\\
\frac{1}{42}=\frac{1}{90}+\frac{1}{p'}\\
\frac{1}{p'}=\frac{1}{42}-\frac{1}{90}
\end{gather}
\]
o Mínimo Múltiplo Comum (M.M.C.) entre 42 e 90 é 630
\[
\begin{gather}
\frac{1}{p'}=\frac{15-7}{630}\\
\frac{1}{p'}=\frac{8}{630}\\
p'=\frac{630}{8}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{p'=78,75\;\text{cm}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .