Exercício Resolvido de Dioptro
publicidade
Um raio de luz incide sobre uma lâmina de faces paralelas sob um ângulo i, o índice de refração da lâmina em relação ao meio envolvente é n e sua espessura e. Determinar o deslocamento lateral do raio luminoso.
Dados do problema:
- Ângulo de incidência do raio de luz: i;
- índice de refração da lâmina em relação ao meio envolvente: \( n=\dfrac{n_{2}}{n_{1}} \);
- espessura da lâmina: e.
Traçamos a normal à primeira face da lâmina e o raio incidente formando o ângulo
\( i={\hat{i}}_{1} \)
com a normal (Figura 1).
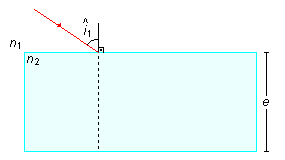
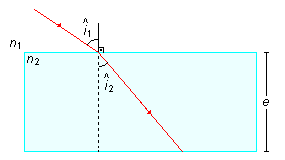
Sendo o meio interno da lâmina mais refringente que o meio externo onde ela está
(n2 > n1) então quando o raio de luz passa do meio externo para o
meio interno ele se aproxima da normal e o ângulo
\( {\hat{i}}_{2} \)
do raio refratado será menor que
\( {\hat{i}}_{1} \)
(Figura 2).
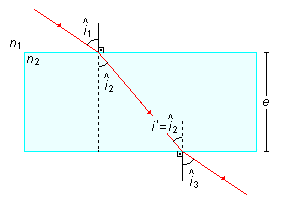
O raio de luz refratado dentro da lâmina vai incidir na segunda face sob um certo ângulo i’,
traçando-se a normal à face no ponto de incidência do raio de luz os ângulo i’ e
\( {\hat{i}}_{2} \)
são alternos internos, então
\( i'={\hat{i}}_{2} \),
o raio sai para o meio externo, passando de um meio mais refringente para um meio menos refringente e ele
se afasta da normal, a direção final será a mesma do raio incidente inicialmente e
\( {\hat{i}}_{3}={\hat{i}}_{1} \)
(Figura 3).
Esquema do problema:
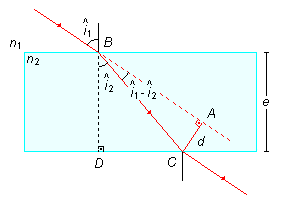
O desvio d será a distância entre os pontos A e C, a distância entre a direção que o raio de luz seguiria se passasse direto, sem desvio, e a direção real que o raio de luz segue após sair da lâmina.
Solução
O desvio d é um dos catetos do triângulo ΔCAB, reto em A, o ângulo (segmento \( \hat{i}_{1}-\hat{i}_{2} \)) é o ângulo entre o caminho que o raio de luz seguiria se não sofresse desvio (segmento (\( \overline{BA} \))) e o raio de luz que atravessa a lâmina (segmento (\( \overline{BC} \))), podemos obter d através do seno do ângulo
\[
\begin{gather}
\operatorname{sen}\left({\hat{i}}_{1}-{\hat{i}}_{2}\right)=\frac{\overline{AC}}{\overline{BC}}=\frac{d}{\overline{BC}} \tag{I}
\end{gather}
\]
O triângulo ΔBDC é reto em D, então o cosseno do ângulo
\( {\hat{i}}_{2} \)
será
\[
\begin{gather}
\cos{\hat{i}}_{2}=\frac{\overline{BD}}{\overline{BC}}=\frac{e}{\overline{BC}} \tag{II}
\end{gather}
\]
onde o cateto
\( \overline{BD} \)
do triângulo é igual a espessura e da lâmina.Das expressões (I) e (II) podemos isolar o lado \( \overline{BC} \) comum aos dois triângulos
\[
\overline{BC}=\frac{d}{\text{sen}\left({\hat{i}}_{1}-{\hat{i}}_{2}\right)}
\]
\[
\overline{BC}=\frac{e}{\cos {\hat{i}}_{2}}
\]
igualando as duas expressões acima
\[
\begin{gather}
\frac{d}{\operatorname{sen}\left({\hat{i}}_{1}-{\hat{i}}_{2}\right)}=\frac{e}{\cos{\hat{i}}_{2}}\\
d=e\frac{\operatorname{sen}\left({\hat{i}}_{1}-{\hat{i}}_{2}\right)}{\cos{\hat{i}}_{2}}
\end{gather}
\]
A espessura (e) e o ângulo de incidência
\( {\hat{i}}_{1} \)
são conhecidos o único dado desconhecido nesta expressão é o ângulo do raio refratado
\( {\hat{i}}_{2} \),
desenvolvendo o termo do seno da diferença que é do tipo
\( \operatorname{sen}(a-b)=\operatorname{sen}a\cos b-\operatorname{sen}b\cos a \)
\( \operatorname{sen}(a-b)=\operatorname{sen}a\cos b-\operatorname{sen}b\cos a \)
, temos
\[
\begin{gather}
d=e\frac{\operatorname{sen}{\hat{i}}_{1}\cos{\hat{i}}_{2}-\operatorname{sen}{\hat{i}}_{2}\cos {\hat{i}}_{1}}{\cos{\hat{i}}_{2}}\\[5pt]
d=e\left[\frac{\operatorname{sen}{\hat{i}}_{1}\cos{\hat{i}}_{2}}{\cos {\hat{i}}_{2}}-\frac{\operatorname{sen}{\hat{i}}_{2}\cos{\hat{i}}_{1}}{\cos{\hat{i}}_{2}}\right]\\[5pt]
d=e\left[\operatorname{sen}{\hat{i}}_{1}-\frac{\operatorname{sen}{\hat{i}}_{2}\cos{\hat{i}}_{1}}{\cos {\hat{i}}_{2}}\right] \tag{III}
\end{gather}
\]
Pela Lei de Snell-Descartes (leia-se isnél-decárte)
\[ \bbox[#99CCFF,10px]
{n_{1}\operatorname{sen}\theta_{1}=n_{2}\operatorname{sen}\theta _{2}}
\]
então podemos correlacionar os ângulos de incidência
\( {\hat{i}}_{1} \)
e refração
\( {\hat{i}}_{2} \)
e isolar o
\( \operatorname{sen}{\hat{i}}_{2} \)
\[
\begin{gather}
n_{1}\operatorname{sen}{\hat{i}}_{1}=n_{2}\operatorname{sen}{\hat{i}}_{2}\\
\operatorname{sen}{\hat{i}}_{2}=\frac{n_{1}}{n_{2}}\operatorname{sen}{\hat{i}}_{1}
\end{gather}
\]
o termo
\( \frac{n_{1}}{n_{2}} \)
é o inverso do índice de refração relativa dado no problema
\( \frac{1}{n}=\frac{n_{1}}{n_{2}} \)
e podemos escrever
\[
\begin{gather}
\operatorname{sen}{\hat{i}}_{2}=\frac{1}{n}\operatorname{sen}{\hat{i}}_{1} \tag{IV}
\end{gather}
\]
Para encontrarmos
\( \cos {\hat{i}}_{2} \)
lembremos da relação trigonométrica
\[
\begin{gather}
\cos^{2}{\hat{i}}_{2}+\operatorname{sen}^{2}{\hat{i}}_{2}=1\\
\cos{\hat{i}}_{2}=\sqrt{1-\operatorname{sen}^{2}{\hat{i}}_{2}}
\end{gather}
\]
substituindo
\( \operatorname{sen}{\hat{i}}_{2} \)
pelo valor encontrado em (IV)
\[
\begin{gather}
\cos{\hat{i}}_{2}=\sqrt{1-\left(\frac{1}{n}\operatorname{sen}{\hat{i}}_{1}\right)^{2}}\\
\cos{\hat{i}}_{2}=\sqrt{1-\frac{1}{n^{2}}\operatorname{sen}^{2}{\hat{i}}_{1}}
\end{gather}
\]
colocando o termo
\( \frac{1}{n^{2}} \)
em evidência
\[
\begin{gather}
\cos{\hat{i}}_{2}=\sqrt{\frac{1}{n^{2}}\left(n^{2}-\operatorname{sen}^{2}{\hat{i}}_{1}\right)}\\\cos
{\hat{i}}_{2}=\frac{1}{n}\sqrt{n^{2}-\operatorname{sen}^{2}{\hat{i}}_{1}} \tag{V}
\end{gather}
\]
substituindo as expressões (IV) e (V) na expressão (III)
\[
d=e\left[\operatorname{sen}{\hat{i}}_{1}-\frac{\cancel{\frac{1}{n}}\operatorname{sen}{\hat{i}}_{1}\cos{\hat{i}}_{1}}{\cancel{\frac{1}{n}}\sqrt{n^{2}-\operatorname{sen}^{2}{\hat{i}}_{1}}}\right]
\]
colocando
\( \operatorname{sen}{\hat{i}}_{1} \)
em evidência
\[ \bbox[#FFCCCC,10px]
{d=e\operatorname{sen}{\hat{i}}_{1}\left[1-\frac{\cos{\hat{i}}_{1}}{\sqrt{n^{2}-\operatorname{sen}^{2}{\hat{i}}_{1}}}\right]}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .