Exercício Resolvido de Dioptro
publicidade
Na parte superior do teto de um submarino militar foi colocada uma fonte de luz isotrópica (ou seja, que emite luz igualmente em todas as direções). Quando este submarino está submerso, qual é a fração da luz que emerge da superfície da água do mar, cujo índice de refração é da ordem de 1,34? Despreze a possibilidade que parte da luz seja absorvida pela água.
Dados do problema:
- Índice de refração da água do mar: nm = 1,34;
- Índice de refração do ar: na = 1.

Solução
A luz emitida pela fonte se espalha de forma igual por uma esfera imaginária em torno da fonte , como se vê na Figura 1-A, existe, no entanto, um ângulo limite onde o raio de luz sai rasante à superfície do mar, se um raio emitido pela fonte possuir um ângulo menor que este ângulo limite ele sai para o ar, mas se o ângulo for maior que este, o raio emitido será refletido de volta para o mar. Chamaremos de A1 a área da esfera que envolve toda a luz emitida pela fonte, e, de A2 a área da calota esférica através da qual a luz escapa para o ar.
Da Figura 1-B podemos tirar os seguintes elementos, sendo R o raio da esfera que envolve a fonte, sua área será de
\[ \bbox[#99CCFF,10px]
{A_{1}=4\pi R^{2}}
\]
se h é a altura da calota que fica para fora da água, sua área será
\[ \bbox[#99CCFF,10px]
{A_{2}=2\pi Rh}
\]
θL será o ângulo limite e o raio será igual a
\[
\begin{gather}
R=L+h \tag{I}
\end{gather}
\]
Então a fração (f) de luz que emergirá será dada pela área da calota fora da água
(A2) dividida pela área total da esfera (A1)
\[
\begin{gather}
f=\frac{A_{2}}{A_{1}}=\frac{2\pi Rh}{4\pi R^{2}}=\frac{h}{2R} \tag{II}
\end{gather}
\]
Para determinar a fração de luz que emerge só precisamos obter h.
Na Figura 2 é mostrado um raio que sai da fonte luminosa e emerge com um ângulo limite, traçando uma normal
(N) no ponto onde o raio emerge e aplicando-se a Lei de Snell-Descartes (leia-se isnél-decárte)
\[ \bbox[#99CCFF,10px]
{n_{1}\operatorname{sen}\theta _{1}=n_{2}\operatorname{sen}\theta _{2}}
\]
\[
\begin{gather}
n_{m}\operatorname{sen}\theta_{L}=n_{a}\operatorname{sen}90°\\
\operatorname{sen}\theta_{L}=\frac{n_{a}}{n_{m}}\operatorname{sen}90°
\end{gather}
\]
sendo \( \operatorname{sen}90°=1 \)
\[
\begin{gather}
\operatorname{sen}\theta _{L}=\frac{n_{a}}{n_{m}}.1\\
\operatorname{sen}\theta _{L}=\frac{n_{a}}{n_{m}}\tag{III}
\end{gather}
\]
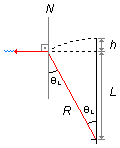
Figura 2
Desta figura também podemos obter o cosseno do ângulo limite
\[
\begin{gather}
\cos \theta _{L}=\frac{\text{cateto adjacente}}{\text{hipoteusa}}=\frac{L}{R}\\
R\cos \theta_{L}=L
\end{gather}
\]
da expressão (I) temos o valor de L=R−h
\[
\begin{gather}
R\cos \theta _{L}=R-h\\
h=R-R\cos \theta_{L}\\
h=R\left(1-\cos \theta _{L}\right) \tag{IV}
\end{gather}
\]
Utilizando a relação trigonométrica
\( \cos ^{2}\theta +\operatorname{sen}^{2}\theta =1 \),
teremos que
\( \cos \theta =\sqrt{1-\operatorname{sen}^{2}\theta \;} \)
substituindo este valor do cosseno na expressão (IV)
\[
h=R\left(1-\sqrt{1-\operatorname{sen}^{2}\theta _{L}\;}\right)
\]
substituindo a expressão (III)
\[
\begin{gather}
h=R\left[1-\sqrt{1-\left(\frac{n_{a}}{n_{m}}\right)^{2}\;}\right] \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (II)
\[
\begin{gather}
f=\frac{R\left[1-\sqrt{1-\left(\dfrac{n_{a}}{n_{m}}\right)^{2}\;}\right]}{2R}\\[5pt]
f=\frac{1}{2}\left[1-\sqrt{1-\left(\frac{n_{a}}{n_{m}}\right)^{2}\;}\right]\\[5pt]
f=\frac{1}{2}\left[1-\sqrt{1-\left(\frac{1}{1,34}\right)^{2}\;}\right]\\
f=0,167
\end{gather}
\]
A fração de luz que emerge do mar será de 16,7%.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .