Exercício Resolvido de Leis de Kepler e Gravitação
publicidade   



Um foguete é lançado da Terra em direção à Lua seguindo uma trajetória retilínea que une os centros dos dois corpos. Sendo a massa da Terra MT aproximadamente 81 vezes maior que a massa da Lua ML, determine o ponto na trajetória em que a intensidade dos campos gravitacionais devido a Terra e a Lua se anulam. Considere o sistema Terra-Lua isolado do resto do Universo, o sistema é estacionário e com a massa total de cada corpo concentrada no seu centro.


Dados do problema:
  • Massa da Terra:    MT;
  • Massa da Lua:    ML;
  • Relação entre as massas da Terra e da Lua:    MT = 81ML .
Esquema do problema:

Como o problema considera as massas da Terra e da Lua concentradas nos seus centros o problema se reduz a dois pontos representando a Terra e a Lua com uma distância d entre eles e o foguete um ponto, de massa m, a uma distância x da Terra (Figura 1).

Figura 1

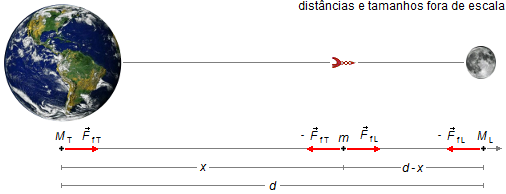
Vamos adotar o sentido positivo orientado da Terra para a Lua.
Entre a Terra e o foguete atua a força de atração gravitacional, \( {\vec{F}}_{fT} \), e entre a Lua e o foguete a força de atração gravitacional, \( {\vec{F}}_{fL} \).

Solução

A força de atração gravitacional é dada pela Lei da Gravitação Universal de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {F_{G}=G\frac{Mm}{r^{2}}} \tag{I} \end{gather} \]
Aplicando a expressão (I) ao sistema Terra-foguete, sendo r = x
\[ \begin{gather} F_{fT}=G\frac{M_{T}m}{x^{2}} \tag{II} \end{gather} \]
Aplicando novamente a expressão (I) ao sistema Lua-foguete, sendo r = d−x
\[ \begin{gather} F_{fL}=G\frac{M_{L}m}{(d-x)^{2}} \tag{III} \end{gather} \]
Para que a intensidade dos campos gravitacionais devido à Terra e à Lua se anulem devemos impor a seguinte condição
\[ \begin{gather} \sum F=0\\ F_{fL}-F_{fT}=0 \end{gather} \]
substituindo as expressões (II) e (III) na expressão acima
\[ \begin{gather} G\frac{M_{L}m}{(d-x)^{2}}-G\frac{M_{T}m}{x^{2}}=0\\[5pt] \cancel{G}\frac{M_{L}\cancel{m}}{(d-x)^{2}}=\cancel{G}\frac{M_{T}\cancel{m}}{x^{2}}\\[5pt] \frac{M_{L}}{(d-x)^{2}}=\frac{M_{T}}{x^{2}} \end{gather} \]
simplificando a Contante Gravitacional Universal G e a massa do foguete m dos dois lados da igualdade, e substituindo a relação entre as massas da Terra e da Lua dada no problema
\[ \begin{gather} \frac{\cancel{M_{L}}}{(d-x)^{2}}=\frac{81 \cancel{M_{L}}}{x^{2}}\\[5pt] \frac{1}{(d-x)^{2}}=\frac{81}{x^{2}}\\[5pt] \frac{x^{2}}{(d-x)^{2}}=81\\[5pt] \left[\frac{x}{d-x}\right]^{2}=81\\[5pt] \frac{x}{d-x}=\sqrt{81\;}\\[5pt] \frac{x}{d-x}=9\\x=9(d-x)\\[5pt] x=9d-9x\\[5pt] x+9x=9d\\[5pt] 10x=9d \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {x=\frac{9}{10}d} \end{gather} \]
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .