Exercício Resolvido de Leis de Kepler e Gravitação
publicidade   



Variações no campo gravitacional na superfície da Terra podem advir de irregularidades na distribuição de sua massa. Considere a Terra como uma esfera de raio R e densidade ρ uniforme, com uma cavidade esférica de raio a, inteiramente contida no seu interior. A distância entre os centros O, da Terra, e C, da cavidade, é d, que pode variar de 0 (zero) até R−a, causando uma variação no campo gravitacional em um ponto P, sobre a superfície da Terra, alinhado com O e C (veja figura). Se G1 é a intensidade do campo gravitacional em P sem a existência da cavidade na Terra, e G2, a intensidade do campo no mesmo ponto, considerando a existência da cavidade. Qual será o valor máximo da variação relativa: \( \left(G_{1}-G_{2}\right)/G_{1} \), que se obtém ao deslocar a posição da cavidade?



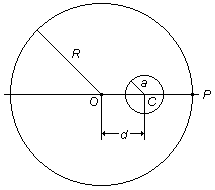
Dados do problema:
  • Raio da Terra:    R;
  • Densidade da Terra:    ρ;
  • Raio da cavidade interna contida na Terra:    a;
  • Distância entre o centro O da Terra e o centro C da cavidade:    d.
Esquema do problema:

Esquema mostrando a Terra em corte com uma cavidade esférica no seu interior.
Figura 1

Solução

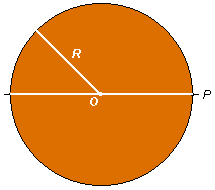
  • Campo gravitacional da Terra sem cavidade
A intensidade do campo gravitacional, G1, da Terra sem a cavidade num ponto P situado a uma distância R do centro é dada por (Figura 2)
\[ \begin{gather} G_{1}=\frac{GM}{R^{2}} \tag{I} \end{gather} \]
onde G é a constante da gravitação universal, M a massa da Terra e V o volume da Terra, a massa é dada por
\[ \begin{gather} M=\rho V \tag{II} \end{gather} \]
Figura 2

o problema considera a Terra como um a esfera, o volume de uma esfera é dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {V=\frac{4}{3}\pi r^{3}} \tag{III} \end{gather} \]
para r = R
\[ \begin{gather} V=\frac{4}{3}\pi R^{3} \tag{IV} \end{gather} \]
substituindo a expressão (IV) na expressão (II), a massa é dada por
\[ \begin{gather} M=\rho \frac{4}{3}\pi R^{3} \tag{V} \end{gather} \]
substituindo a expressão (V) na expressão (I), a intensidade do campo gravitacional da Terra será
\[ G_{1}=\frac{G\rho \frac{4}{3}\pi R^{\cancel{3}}}{\cancel{R^{2}}} \]
simplificando os valores de R3 no numerador e R2 no denominador
\[ \begin{gather} G_{1}=\frac{4}{3}\pi RG\rho \tag{VI} \end{gather} \]
  • Campo gravitacional gerado pela esfera retirada da cavidade
O campo gravitacional, GE, produzido por uma esfera de raio a, massa m, volume v e mesma densidade ρ que a Terra, num ponto P a uma distância (R−d) será (Figura 3)
\[ \begin{gather} G_{E}=\frac{Gm}{(R-d)^{2}} \tag{VII} \end{gather} \]
a massa da esfera é calculada por

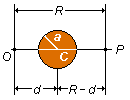
Figura 3
\[ \begin{gather} m=\rho v \tag{VIII} \end{gather} \]
fazendo r = a na expressão (III)
\[ \begin{gather} v=\frac{4}{3}\pi a^{3} \tag{IX} \end{gather} \]
substituindo a expressão (IX) na expressão (VIII) a massa será
\[ \begin{gather} m=\rho \frac{4}{3}\pi a^{3} \tag{X} \end{gather} \]
substituindo a expressão (X) na expressão (VII), o campo da esfera será
\[ \begin{gather} G_{E}=\frac{\dfrac{4}{3}\pi a^{3}G\rho }{(R-d)^{2}}\\ G_{E}=\frac{4}{3}\pi a^{3}G\rho\frac{1}{(R-d)^{2}} \tag{XI} \end{gather} \]
  • Campo gravitacional da Terra com cavidade
O campo gravitacional G2 gerado pela Terra, num ponto P, com a cavidade deixada quando se retira uma esfera do seu interior será dado pelo campo total dado em G1 (equação V) menos o campo GE da esfera retirada do seu interior (equação X)
\[ G_{2}=G_{1}-G_{E}=\frac{4}{3}\pi RG\rho -\frac{4}{3}\pi a^{3}G\rho\frac{1}{(R-d)^{2}} \]
colocando em evidência o termo \( \frac{4}{3}\pi G\rho \) do lado direito da igualdade
\[ \begin{gather} G_{2}=\frac{4}{3}\pi G\rho \left[R-\frac{a^{3}}{(R-d)^{2}}\right] \tag{XII} \end{gather} \]
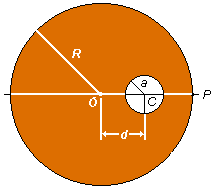
Esta é a expressão do campo gravitacional da Terra com uma cavidade no seu interior num ponto P (Figura 4).
Usando as expressões (VI) e (XII) calcula-se a variação pedida no problema
\[ \frac{G_{1}-G_{2}}{G_{1}}=\frac{\cancel{\dfrac{4}{3}}\cancel{\pi} R \cancel{G}\cancel{\rho} -\cancel{\dfrac{4}{3}}\cancel{\pi} \cancel{G}\cancel{\rho} \left[R-\dfrac{a^{3}}{(R-d)^{2}}\right]}{\cancel{\dfrac{4}{3}}\cancel{\pi} R \cancel{G}\cancel{\rho}} \]
simplificando o termo \( \frac{4}{3}\pi G\rho \) que aparece em todos os termos da expressão
\[ \begin{gather} \frac{G_{1}-G_{2}}{G_{1}}=\frac{R-R+\dfrac{a^{3}}{(R-d)^{2}}}{R}\\[5pt] \frac{G_{1}-G_{2}}{G_{1}}=\frac{a^{3}}{R(R-d)^{2}} \end{gather} \]
Figura 4

A expressão acima fornece a variação relativa do campo gravitacional e terá um valor máximo quando o denominador tiver um valor mínimo. Como R (o raio da Terra é uma constante) então d dever ser máximo para tornar a diferença (R−d) mínima, o enunciado nos diz que d varia de zero (valor mínimo) até R−a (valor máximo), assim d = R−a
\[ \begin{gather} \frac{G_{1}-G_{2}}{G_{1}}=\frac{a^{3}}{R[R-(R-a)]^{2}}\\[5pt] \frac{G_{1}-G_{2}}{G_{1}}=\frac{a^{3}}{R[R-R+a]^{2}}\\[5pt] \frac{G_{1}-G_{2}}{G_{1}}=\frac{a^{\cancel{3}}}{R\cancel{[a]^{2}}} \end{gather} \]
simplificando os termos, a3 no numerador e a2 no denominador, a variação máxima do campo é dada por
\[ \bbox[#FFCCCC,10px] {\frac{G_{1}-G_{2}}{G_{1}}=\frac{a}{R}} \]

Observação: A expressão (I) é obtida a partir da 2.ª Lei de Newton
\[ \bbox[#99CCFF,10px] {F=m a} \]
e da Lei da Gravitação Universal
\[ \bbox[#99CCFF,10px] {F=G\frac{Mm}{r^{2}}} \]
Fazenfo a = g na primeira expressão e igualando as duas expressões
\[ \begin{gather} m g=G\frac{Mm}{r^{2}}\\ g=\frac{GM}{r^{2}} \end{gather} \]
esta expressão fornece a aceleração da gravidade em qualquer corpo, conhecidos a sua massa M e o seu raio r.
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .