Exercício Resolvido de Dinâmica
publicidade
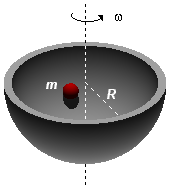
Uma pequena esfera de massa m é introduzida num recipiente cuja superfície interna é um hemisfério
de raio R. O recipiente gira em torno do eixo vertical com velocidade angular ω.
Determinar:
a) A intensidade da força que a esfera faz contra a parede;
b) O raio da circunferência descrita pela esfera quando em equilíbrio em relação ao recipiente.
a) A intensidade da força que a esfera faz contra a parede;
b) O raio da circunferência descrita pela esfera quando em equilíbrio em relação ao recipiente.
Dados do problema:
- Massa da esfera: m;
- Raio do hemisfério: R;
- Velocidade angular do hemisfério: ω.
O recipiente está girando e a esfera no seu interior fica equilibrada a uma determinada altura na superfície interma. Este sistema é equivalente a um recipiente em repouso com uma esfera girando no seu interior com velocidade ω.
As forças que atuam na esfera são a força peso \(\vec{P} \) verticalmente para baixo, a força normal de reação \( \vec{N} \) perpendicular à parede do hemisfério, apontada para o centro do hemisfério (Figura 1-A).
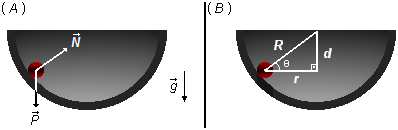
O hemisfério possui um raio R, a distância d é medida entre o centro do hemisfério e o centro da circunferência de raio r descrita pela esfera (Figura 1-B).
Solução
Desenhando as forças em um sistema de eixos coordenados xy podemos aplicar a
2.ª Lei de Newton para o movimento circular
\[
\begin{gather}
\bbox[#99CCFF,10px]
{{\vec F}_{cp}=m{\vec a}_{cp}} \tag{I}
\end{gather}
\]
a) A força que a esfera faz contra a parede do hemisfério é igual, em intensidade, a força que o
hemisfério faz sobre a esfera. Estas forças formam um par de forças de ação e reação, conforme a
3.ª Lei de Newton.

Figura 2
A força centrípeta resultante \( {\vec{F}}_{cp} \) é dada pela componente da força normal na direção x, \( {\vec N}_{x} \) (Figura 2)
\[
\begin{gather}
F_{cp}=N_{x} \tag{II}
\end{gather}
\]
a componente Nx é dada por
\[
\begin{gather}
N_{x}=N\cos \theta \tag{III}
\end{gather}
\]
o cosseno será dado por (Figura 1-B)
\[
\begin{gather}
\cos \theta =\frac{r}{R} \tag{IV}
\end{gather}
\]
substituindo a expressão (IV) na expressão (III)
\[
\begin{gather}
N_{x}=N\frac{r}{R} \tag{V}
\end{gather}
\]
A aceleração centrípeta é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_{cp}=\frac{v^{2}}{r}} \tag{VI}
\end{gather}
\]
a velocidade em função da velocidade angular é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r} \tag{VII}
\end{gather}
\]
substituindo a expressão (VII) na expressão (VI)
\[
\begin{gather}
a_{cp}=\frac{(\omega r)^{2}}{r}\\[5pt]
a_{cp}=\frac{\omega^{2}r^{\cancel{2}}}{\cancel{r}}\\[5pt]
a_{cp}=\omega^{2}r \tag{VIII}
\end{gather}
\]
Substituindo as expressões (V) e (VIII) na expressão (I)
\[
\begin{gather}
N\frac{\cancel{r}}{R}=m\omega^{2}\cancel{r}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{N=Rm\omega ^{2}}
\end{gather}
\]
b) Na direção y não há movimento, a força peso \( \vec{P} \) e a componente da força normal de reação \( {\vec N}_{y} \) se anulam.
\[
\begin{gather}
P=N_{y} \tag{IX}
\end{gather}
\]
a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{X}
\end{gather}
\]
a componente Ny é dada por
\[
\begin{gather}
N_{y}=N\operatorname{sen}\theta \tag{XI}
\end{gather}
\]
o seno será dado por (Figura 1-B)
\[
\begin{gather}
\operatorname{sen}\theta =\frac{d}{R} \tag{XII}
\end{gather}
\]
substituindo a expressão (XII) e o resultado da força normal encontrada no item anterior na expressão (XI)
\[
\begin{gather}
N_{y}=Rm\omega ^{2}\frac{d}{R} \tag{XIII}
\end{gather}
\]
substituindo as expressões (X) e (XIII) na expressão (IX)
\[
\begin{gather}
\cancel{m}g=\cancel{R}\cancel{m}\omega^{2}\frac{d}{\cancel{R}}\\[5pt]
g=\omega ^{2}d\\[5pt]
d=\frac{g}{\omega ^{2}} \tag{XIV}
\end{gather}
\]
Aplicando o Teorema de Pitágoras ao triângulo da Figura 1-B
\[
\begin{gather}
R^{2}=d^{2}+r^{2}
\end{gather}
\]
substituindo o valor de d encontrado em (XIV)
\[
\begin{gather}
R^{2}=\left(\frac{g}{\omega^{2}}\right)^{2}+r^{2}\\[5pt]
R^{2}=\frac{g^{2}}{\omega^{4}}+r^{2}\\[5pt]
r^{2}=R^{2}-\frac{g^{2}}{\omega ^{4}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{r=\sqrt{R^{2}-\frac{g^{2}}{\omega ^{4}}\;}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .