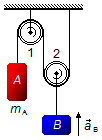
No sistema da figura, as polias 1 e 2 são ideais, a polia 1 é fixa e a polia 2 é móvel. O bloco A
possui massa 11 kg e o bloco B sobe com aceleração 1 m/s2. Determinar a aceleração do
bloco A, a massa do bloco B e a tensão na corda. Adote a aceleração da gravidade igual à
10 m/s2.
Dados do problema:
- Massa do corpo A: mA = 11 kg;
- Aceleração do corpo B: aB = 1 m/s2;
- Aceleração da gravidade: g = 10 m/s2.
Esquema do problema:
A força peso do corpo A
\( {\vec P}_{\small A} \)
produz uma tração
\( \vec T \)
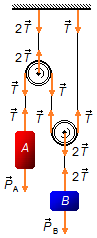
na corda, esta é transferida pela corda para o outro lado da polia fixa no teto. Esta tração é
transmitida pela corda que passa pela segunda polia (móvel) para o outro lado da polia. Para equilibrar
estas duas trações temos na corda que sai da polia uma tração igual a
\( 2\vec T \),
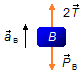
esta tração atua na corda que prende o corpo B onde atua a força peso do corpo B
\( {\vec P}_{\small B} \)
(Figura 1).
Solução:
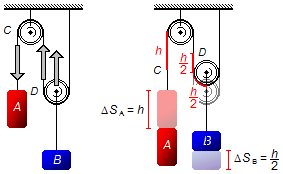
Quando o bloco
A desce uma distância
h um ponto
C da corda desce
h
(Figura 2), como esta polia está fixa no teto, a corda do outro lado da polia sobe
h. Como a
segunda polia está livre, um ponto
D na corda deve subir
h, deste valor
\( \frac{h}{2} \)
são o deslocamento do ponto, em relação a polia, e os outros
\( \frac{h}{2} \)
são resultante da subida da própria polia que é puxada para cima. Então temos a condição
\[
\begin{gather}
\Delta S_{\small A}=2\Delta S_{\small B} \tag{I}
\end{gather}
\]
Da Cinemática Escalar temos que um corpo se movimentando sob a ação de uma aceleração constante está
em Movimento Retilíneo Uniformemente Variado (M.R.U.V.) descrito pela equação horária
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
\[
\begin{gather}
S-S_0=v_0t+\frac{a}{2}t^2
\end{gather}
\]
como
\( \Delta S=S-S_0 \)
\[
\begin{gather}
\Delta S=v_0t+\frac{a}{2}t^2 \tag{II}
\end{gather}
\]
Escrevendo a equação (II) para cada um dos blocos
\[
\begin{gather}
\Delta S_{\small A}=v_{0\small A}t+\frac{a_{\small A}}{2}t^2 \tag{III-a} \\[10pt]
\Delta S_{\small B}=v_{0\small B}t+\frac{a_{\small B}}{2}t^2 \tag{III-b}
\end{gather}
\]
adotando que os blocos partem do repouso, suas velocidades serão nulas,
\( v_{0\small A}=v_{0\small B}=0 \),
substituindo estes valores as equações (III-a) e (III-b) se reduzem a
\[
\begin{gather}
\Delta S_{\small A}=0\times t+\frac{a_{\small A}}{2}t^2 \\[5pt]
\Delta S_{\small A}=\frac{a_{\small A}}{2}t^2 \tag{IV-a} \\[10pt]
\Delta S_{\small B}=0\times t+\frac{a_{\small B}}{2}t^2 \\[5pt]
\Delta S_{\small B}=\frac{a_{\small B}}{2}t^2 \tag{IV-b}
\end{gather}
\]
substituindo as equações (IV-a) e (IV-b) na condição (I)
\[
\begin{gather}
\frac{a_{\small A}}{2}t^2=2\times\frac{a_{\small B}}{2}t^2 \\[5pt]
\frac{a_{\small A}}{2}t^2=a_{\small B}t^2 \\[5pt]
a_{\small A}\cancel{t^2}=2a_{\small B}\cancel{t^2} \\[5pt]
a_{\small A}=2a_{\small B}
\end{gather}
\]
substituindo o valor da aceleração do corpo B dado
\[
\begin{gather}
a_{\small A}=2\times 1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_{\small A}=2\;\mathrm{m/s^2}}
\end{gather}
\]
Isolando os corpos e pesquisando as forças que atuam em cada um deles aplicamos a
2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a} \tag{V}
\end{gather}
\]
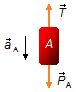
Corpo A:
- \( {\vec P}_{\small A} \): força peso do corpo A;
- \( \vec T \): força de tensão na corda.
Adotamos o sentido positivo no mesmo sentido da aceleração. Na direção horizontal não há forças atuando,
na direção vertical aplicando a equação (V)
\[
\begin{gather}
P_{\small A}-T=m_{\small A}a_{\small A} \tag{VI}
\end{gather}
\]
Corpo B:
- \( {\vec P}_{\small B} \): peso do corpo B;
- \( \vec T \): tensão na corda.
Adotamos o sentido positivo no mesmo sentido da aceleração. Na direção horizontal não há forças atuando,
na direção vertical aplicando a equação (V)
\[
\begin{gather}
2T-P_{\small B}=m_{\small B}a_{\small B} \tag{VII}
\end{gather}
\]
As equações (VI) e (VII) formam um sistema de duas equações a duas incógnitas,
T e mB
\[
\begin{gather}
\left\{
\begin{matrix}
P_{\small A}-T=m_{\small A}a_{\small A} \\
2T-P_{\small B}=m_{\small B}a_{\small B}
\end{matrix}
\right.
\end{gather}
\]
multiplicando a primeira equação por 2 e somando as duas equações
\[
\begin{gather}
\qquad\;\;\left\{
\begin{array}{l}
\;P_{\small A}-T=m_{\small A}a_{\small A}\qquad (\times 2) \\
\;2T-P_{\small B}=m_{\small B}a_{\small B}
\end{array}
\right. \\[10pt]
\frac{
\begin{matrix}
\;2P_{\small A}-\cancel{2T}=2m_{\small A}a_{\small A} \\
\;\cancel{2T}-P_{\small B}=m_{\small B}a_{\small B}
\end{matrix}
}
{2P_{\small A}-P_{\small B}=2m_{\small A}a_{\small A}+m_{\small B}a_{\small B}} \tag{VIII}
\end{gather}
\]
A força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{IX}
\end{gather}
\]
Aplicando a equação (IX) aos corpos A e B
\[
\begin{gather}
P_{\small A}=m_{\small A}g \tag{X-a}
\end{gather}
\]
\[
\begin{gather}
P_{\small B}=m_{\small B}g \tag{X-b}
\end{gather}
\]
substituindo as equações (X-a) e (X-b) na equação (VIII)
\[
\begin{gather}
2m_{\small A}g-m_{\small B}g=2m_{\small A}a_{\small A}+m_{\small B}a_{\small B} \\[5pt]
m_{\small B}a_{\small B}+m_{\small B}g=2m_{\small A}g-2m_{\small A}a_{\small A}
\end{gather}
\]
colocando o termo −mB em evidência do lado esquerdo da igualdade
e 2mA do lado direito
\[
\begin{gather}
m_{\small B}\left(a_{\small B}+g\right)=2m_{\small A}\left(g-a_{\small A}\right) \\[5pt]
m_{\small B}=\frac{2m_{\small A}\left(g-a_{\small A}\right)}{\left(a_{\small B}+g\right)}
\end{gather}
\]
substituindo os valores dados no problema e a aceleração do corpo A encontrada acima
\[
\begin{gather}
m_{\small B}=\frac{2\times 11\times\left(10-2\right)}{\left(1+10\right)} \\[5pt]
m_{\small B}=\frac{22\times\left(8\right)}{11} \\[5pt]
m_{\small B}=2\times 8
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{m_{\small B}=16\;\mathrm{kg}}
\end{gather}
\]
Na equação (VI) isolando o valor da força de tensão e substituindo a força peso do corpo A pelo
valor dado em (X-a)
\[
\begin{gather}
T=m_{\small A}g-m_{\small A}a_{\small A} \\[5pt]
T=11\times 10-11\times 2 \\[5pt]
T=110-22 \\[5pt]
T=88\;\mathrm N
\end{gather}
\]
A tração na corda presa ao corpo A será de
T = 88 N
e a tração na corda presa ao corpo B será de
2T = 2\times 88 = 176 N.
EN
